電気に関する基礎理論
「電気に関する基礎理論」の内容は,①「電流,電圧,電力及び電気抵抗」,②「導体及び絶縁体」,③「交流電気の基礎概念」,④「電気回路の計算」である。
この科目では,電気工事士だけではなく,電気技術者を志す全ての方が理解しておくべき電気に関する基本的な事項が問われる。電気は社会生活に欠かせないエネルギーであると同時に,扱いを間違えると,感電,火災等の危険もある。その電気を扱う専門技術者にとって,オームの法則をはじめとする電気の基礎理論を十分に理解しておかなければならない。
電流,電圧,電力及び電気抵抗
電流(Current)
電流 $i$ [A] は電荷 $q$ [C] の時間変化として定義される。
\[ i = \frac{\text{d}q}{\text{d}t} \]上式によれば,電荷 $q$ [C] の時間変化が大きければ,電流 $i$ [A] は大きくなる。また,電流の向きは,正の電気の動く向きとされているため,下図のように,電流の向きは自由電子が移動する向きとは逆になる。

電荷 $q$ の単位としてクーロンが用いられ,記号 C で表される。また,電流 $i$ の単位としてクーロン/秒すなわちアンペアが用いられ,記号 A で表される。時間的に変化しない電流 $I$ を直流電流といい,周期的に大きさと向きが変化する電流 $i$ を交流電流という。
ちなみに,国際単位系(SI)[1]において,電流 アンペア(A)は,次のように定義されている。
アンペア(記号 A)は,電流の SI 単位であり,電気素量 $e$ を単位 C(A s に等しい)で表したときに,その数値を 1.602 176 634 × 10-19 と定めることによって定義される。ここで,秒は $\Delta v_\text{Cs}$ によって定義される。
この定義は $e$ = 1.602 176 634 × 10-19 A s という厳密な関係を示している。この式から定義定数 $e$ および $\Delta v_\text{Cs}$ を用いてアンペアを以下のように厳密に表現することができる。
\[ 1 \text{ A} = (\frac{e}{1.602 176 634 \times 10^{-19}}) \text{ s}^{-1} \](参考)アンペアの由来
電流の単位であるアンペアは,フランスの物理学者・数学者で,電磁気学の創始者の一人であるアンドレ=マリ・アンペール(1775 - 1836 年)にちなんでいる。

(出典)フリー百科事典 ウィキペディア
(参考)電流の定義の変遷
1908年に万国電気単位本会議で国際電気単位が定められた。このとき,電流については「硝酸銀溶液に電流を通した際,1 秒間に 0.001 118 00 g の銀を析出する不変電流」を 1 A として定義し,一次標準器として「銀分離器」が利用されてきた。
この後,電流天秤や相互誘導によりこれら標準の絶対測定が行われ,この標準の確かさ,cgs 単位系[2]との一致の確かさが確認されていった。一方で当時,メートル条約で定められた MKS 単位系[3]と国際電気単位を統合し MKSA 単位系[4]としてまとめる動きが国際的に高まった。
そのような背景があり,1948年に開催された第9回国際度量衡総会によって,電流の定義は「真空中に 1 メートルの間隔で平衡に配置された無限に小さい円形断面を有する無限に長い 2 本の直線状導体のそれぞれを流れ,これらの導体の長さ 1 メートルにつき 2 × 10-7 ニュートンの力を及ぼしあう一定の電流である」と変更された。この電流の定義は,実際の電流標準器作製法を定めたものではなく,むしろ真空の透磁率を $\mu_0 \equiv 4 \pi \times 10^{-7}$ m kg s-2 A-2 と定義することによって国際単位系の一貫性を担保するように定められたものである。
- 国際単位系(International System of Units : SI)は,メートル法の後継として国際的に定められ,世界中で広く使用されている単位系である。
- CGS 単位系は,長さの単位としてのセンチメートル(centimetre),質量の単位としてのグラム(gram),時間の単位としての秒(second)を基本単位とする,一貫性のあるメートル法系の単位法である。MKS 単位系,国際単位系(SI)に置き換えられたが,特定の分野では CGS 単位系の単位が残っている。
- MKS 単位系とは,長さの単位メートル(metre : m),質量の単位キログラム(kilogram : kg),時間の単位秒(second : s)を基本単位とする,一貫性のある単位系である。
- MKS 単位系に 4 つ目の基本単位としてアンペア(ampere : A)を追加した単位系である。MKS は力学のみを扱えるが,電流の単位アンペアを追加することで,電磁気学を扱うことができる。
電圧(Voltage)
電位差のある 2 点を導体で結べば,電位の高い方から電位の低い方へと電荷が移動して電流が生ずる。電位差を発生させる装置の一つとして電池があり,起電力を持っているという。起電力 $E$ と電圧 $V$ は単位としてボルトが用いられ,記号 V で表される。時間的に不変である電圧 $V$ を直流電圧,周期的に大きさと向きが変化する電圧 $v$ を交流電圧という。1 V は,1 A の不変の電流が流れる導体の 2 点間において消費される電力が 1 W であるとき,その 2 点間の電圧,交流電圧では,電圧の瞬時値の 2 乗の 1 周期平均の平方根が上記の値に等しい電圧である。
(参考)ボルトの由来
電圧の単位であるボルトは,ボルタ電池を発明したイタリアの物理学者アレッサンドロ・ボルタ(1745 - 1827 年)に由来する。

(出典)フリー百科事典 ウィキペディア
電力(Power)
熱エネルギーへの変換
抵抗器が消費する電力 $P$ は,抵抗器の両端の電圧 $v$ と抵抗器に流れる電流 $i$ の積で表される。オームの法則より,電力は電流の 2 乗と抵抗の積,または電圧の 2 乗を抵抗で除した形でも表される。
\[ P = vi \]ここに,$R$ にかかる電圧 $v$ は $Ri$ であり,$i$ は $Gv$ であるから,電力 $P$ は次式で表される。
\[ P = vi = Ri^2 = Gv^2 = \frac{i^2}{G} = \frac{v^2}{R} \]電力 $P$ の単位はワットで与えられ,記号 W で表される。
(参考)ワットの由来
電力の単位であるワットは,蒸気機関の発展に大いに貢献したスコットランド出身の発明家であり,機械技術者でもあるジェームズ・ワット(1736 - 1819 年)に由来する。

(出典)フリー百科事典 ウィキペディア
電力量(electric energy)
電力 $P$ は毎秒に消費される電力量であるから,ある時間 $t$ の間に消費される電力量 $w$ は次式で表される。
\[ w = Pt = vit \]$P$ の単位を W ,$t$ の単位を s としたとき,電力量 $w$ の単位はジュールで与えられ,記号 J で表される。実用的な単位としてワット時(watt-hour)が用いられ,記号 W·h で表される。ちなみに,1 ジュールは「1 ニュートンの力がその力の方向に物体を 1 メートル動かすときの仕事」と定義される。
熱量と電力量の換算
電力量 1 ワット秒は,熱量 1 ジュールに等しく,電力量 1 ワット時は,熱量 3 600 ジュールに等しい。
ここで,1 時間は 3,600 秒(60 分/時間 × 60 秒/分)である。
(参考)ジュールの由来
エネルギー,仕事,熱量,電気量の単位であるジュールは,イギリスの物理学者ジェームズ・プレスコット・ジュール(1818 - 1889 年)に由来する。
ジュール熱量 $Q$ [J] は,電流 $I$ [A] が抵抗 $R$ [Ω] に $t$ [秒] 流れたとき発生する熱量で,次式で表される。
\[ Q = RI^2 t \]
(出典)フリー百科事典 ウィキペディア
過去問題
- 2019年度 下期 No. 3 発熱量
- 2019年度 上期 No. 3 水の温度上昇に必要な電力量
- 平成30年度(2018年度) 下期 No. 4 水の温度上昇に必要な電力量
- 平成30年度(2018年度) 上期 No. 4 電線の接触不良により発生する熱量
- 平成25年度(2013年度) 下期 No. 4 電線の接続不良により発生する熱量
抵抗(resistance)
加えられた電気エネルギーを蓄積することなく消費する素子を抵抗素子といい,下図に示す図記号で表す。定義は「1 V の電圧をかけたときに 1 A の電流が流れる電気抵抗」である。


(参考)オームの由来
抵抗の単位であるオームは,電気抵抗に関するオームの法則を発見したドイツの物理学者ゲオルク・ジーモン・オーム(1789 - 1854 年)に由来する。

(出典)フリー百科事典 ウィキペディア
インダクタンス素子(inductance)
加えられた電気エネルギーを一時的に電磁エネルギーに変換する素子をインダクタンス素子または誘導素子という。

インダクタンス素子における変化する電圧 $v$ と変化する電流 $i$ の関係は,次式で表される。ここに,比例定数 $L$ をインダクタンスといい,単位としてヘンリーが用いられ,記号 H で表される。定義は「1 秒間に 1 A の割合で変化する直流の電流が流れるときに 1 V の起電力を生ずる閉回路のインダクタンス」である。
\[ v = L \frac{\text{d}i}{\text{d}t} \](参考)ヘンリーの由来
インダクタンスの単位であるヘンリーは,アメリカ合衆国の物理学者ジョセフ・ヘンリー(1797 - 1878 年)に由来する。

(出典)フリー百科事典 ウィキペディア
キャパシタンス素子(capacitance)
静電エネルギーを蓄積する素子をキャパシタンス素子または静電容量素子という。

キャパシタンス素子における電圧 $v$ と変化する電流 $i$ の関係は,次式で表される。ここに,比例定数 $C$ をキャパシタンスまたは静電容量といい,単位としてファラドが用いられ,記号 F で表される。定義は「1 C の電気量を充電したときに 1 V の直流の電圧を生じる 2 導体間の静電容量」である。
\[ i = C \frac{\text{d}v}{\text{d}t} \](参考)ファラドの由来
キャパシタンスの単位であるファラドは,イギリスの化学者・物理学者で,電磁気学および電気化学の分野での貢献が知られているマイケル・ファラデー(1791 - 1867 年)に由来する。

(出典)フリー百科事典 ウィキペディア
実用電気単位系の定義
実用電気単位系の定義は次表のようにまとめられる。
| 量 | 単位の名称 | 記号 | 定義 |
|---|---|---|---|
| 電流 | アンペア | A | アンペアは,電流の SI 単位である。これは,単位 C(A s に等しい)による表現において,電気素量 $e$ を正確に 1.602 176 634 × 10-19 と定めることによって設定される。 |
| 電圧 | ボルト | V | 1 V は,1 A の不変の電流が流れる導体の 2 点間において消費される電力が 1 W であるとき,その 2 点間の電圧,交流電圧では,電圧の瞬時値の 2 乗の 1 周期平均の平方根が上記の値に等しい電圧 |
| 電力 | ワット | W | 1 W は,毎秒 1 ジュールの割合でエネルギーを出す仕事効率 |
| 抵抗 | オーム | Ω | 1 Ω は,1 A の電流が流れる導体の 2 点間の電圧が 1 V であるときその 2 点間の電気抵抗 |
| インダクタンス | ヘンリー | H | 1 H は,1 A/s の割合で一様に変化する電流が流れるときに,1 V の起電力を生じる閉回路のインダクタンス |
| 静電容量 | ファラド | F | 1 F は,1 C の電気量を充電したときに 1 V の電圧を生じるコンデンサの静電容量 |
導体及び絶縁体
導体(conductor)
電気伝導体は,移動可能な電荷を含み電気を通しやすい材料,すなわち電気伝導率(導電率)の高い材料である。良導体,単に導体とも呼ぶ。
下図に示す断面積が円形の導体(電線)の抵抗 $R$ [Ω] は,抵抗率 $\rho$ [Ω·mm²/m],電線の長さ $l$ [m],電線の断面積 $A$ [mm²](電線の直径 $D$ [mm])を用いて次式で表される。
\[ R = \rho \frac{l}{A} = \rho \frac{4l}{\pi D^2} \]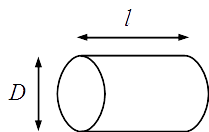
電線の抵抗は抵抗率,電線の長さに比例し,電線の断面積(または電線の半径の二乗)に反比例する。同じ抵抗率の材料を用いるならば,電線の抵抗を小さくするためには,電線を短く,そして太くすればよい。
また,抵抗率の逆数を導電率(electric conductivity)と呼び,相対の導電度を表すのに用いられる。
銅は,導電率および熱伝導率が高く,しかも腐食に対しても非常に安定していてそのうえ比較的安価なので,電気機器の導電材料として最も重要なものの一つである。銅は,電気機器の巻線をはじめ,導電部分の主要材料として,主として丸線,平角線,あるいは銅帯の形で使用されるが,場合により銅棒または銅網の形で使用されることもある。
銀は,導電率は最も高いが効果であり,またアルミニウムは銅に比べて導電率が非常に低いため,機器の巻線用としては不適当である。
| 導体 | 抵抗率 [Ω·m] |
|---|---|
| 銀 | 1.59 × 10-8 |
| 銅 | 1.68 × 10-8 |
| アルミニウム | 2.65 × 10-8 |
| 鉄 | 1.00 × 10-7 |
電線の許容電流
電線の許容電流については,次のようになる。
- 許容電流は,周囲の温度が上昇すると,小さくなる。
- 許容電流は,導体の直径が大きくなると,大きくなる。
例題
直径 2.6 mm,長さ 20 m の銅導線と抵抗値が最も近い同材質の銅導線は。
解答・解説
直径 2.6 mm,長さ 20 m の銅導線と抵抗値は,次式で求められる。
\[ R = \rho \frac{4l}{\pi D^2} = \rho \frac{4 \times 20}{\pi 2.6^2} = 3.77 \rho \]同様にイ,ロ,ハ,二の抵抗値($R_1$,$R_2$,$R_3$,$R_4$)を求める。
\[ R_1 = \rho \frac{4l}{\pi D^2} = \rho \frac{4 \times 40}{\pi 1.6^2}=19.9 \rho \] \[ R_2 = \rho \frac{l}{A} = \rho \frac{20}{8} = 2.5 \rho \] \[ R_3 = \rho \frac{4l}{\pi D^2} = \rho \frac{4 \times 10}{\pi 3.2^2} = 1.24 \rho \] \[ R_4 = \rho \frac{l}{A} = \rho \frac{20}{5.5} = 3.64 \rho \]正解はニ.断面積 5.5 mm2,長さ 20 mである。
過去問題
- 2019年度 下期 No. 2 電線の抵抗
- 2019年度 上期 No. 2 電線の抵抗と許容電流
- 平成30年度(2018年度) 下期 No. 3 銅導線の抵抗値
- 平成30年度(2018年度) 上期 No. 3 電線の抵抗と許容電流
- 平成25年度(2013年度) 下期 No. 3 銅導線の抵抗値
- 平成25年度(2013年度) 上期 No. 2 銅導線の抵抗値
絶縁体(insulator)
絶縁体は,電気あるいは熱を通しにくい性質を持つ物質の総称である。自由電子の移動が少ない物質は,絶縁体として分類される。ゴム,ガラス,プラスチック,木,油なども絶縁体である。
交流電気の基礎概念
下図のような波形を持つ電圧 $v$ は数学的に
\[ v=V_\text{m} \sin(\omega t - \theta) \]で表すことができる。$v$ は任意の時刻における電圧を表しているから,これをその電圧の瞬時値(instantaneous value)と呼ぶ。$V_\text{m}$ は電圧の最大の値を表しているから,これを最大値(maximum value)または振幅(amplitude)と呼ぶ。ある任意の時刻 $t$ に値 $v$ となり,それより時刻 $T$ を経るごとに再び $v$ となる。このように 1 波形を完了するに要する時間 $T$ を,その正弦波の周期(period)と呼ぶ。一方,正弦波関数には $\sin x = \sin(x+2\pi)$ の関係があり,角(平面角)について $2\pi$ [rad] の周期を持っているから,これを上述の場合に比較すれば,$\omega T = 2\pi$ でなければならない。すなわち次式の関係がある。
\[ \omega = \frac{2\pi}{T} \text{ [rad/s]} \]この $\omega$ を角速度(angular velocity)あるいは角周波数(angular frequency)という。また,単位時間(一般に 1 秒間)に同一波形を繰り返す回数を周波数(frequency)といい,これを $f$ とすれば,
\[ f=\frac{1}{T} \text{ [Hz]} \]となり,周波数 $f$ と角周波数 $\omega$ との間には,次式の関係がある。
\[ \omega = 2\pi f \]わが国における商用交流の周波数には主として 50 Hz と 60 Hz が用いられる。このような周波数を一般に商用周波数(commercial frequency)と呼んでいる。

周波数(frequency)
交流では電流の向きが周期的に正・負に代わるが,この 1 秒間の繰り返し数を周波数と呼び,単位としては Hz(ヘルツ)を用いる。世界的にみた場合,電気事業が供給している電気の周波数は 50 Hz(ヨーロッパ系)または 60 Hz(アメリカ系)のどちらかに集約されており,わが国でも電気事業の発展の歴史的背景から,東地域(北海道・東北・東京)が 50 Hz,中・西地域(中部,北陸,関西,中国,四国,九州)が 60 Hz の系統周波数に大きく分かれている。わが国では電気事業法によって,供給する電気の周波数を一定値(供給する電気の標準周波数に等しい値,すなわち 50 Hz または 60 Hz)に維持することとされており,周波数の測定と記録保存が義務づけられている。周波数の変動は,モータの回転速度等に影響を与えるが,現状では平常時ではほとんどの場合,標準周波数に対して ±0.1 Hz 以内の変動範囲におさまっている。
$RL$ 直列回路
下図のように抵抗 $R$,インダクタンス $L$ を直列に接続した回路に交流電源電圧 $e$ を加えたとき,電流 $i$ が流れたとすれば,次式が成り立つ。
\[ L \frac{\text{d}i}{\text{d}t} + Ri = e \]
$e = E_\text{m}\sin(\omega t - \theta)$ の交流電源電圧を加えたとすれば,瞬時電流 $i$ は次式となる。$\phi$ は,電圧,電流の位相差である。
\[ i = \frac{E_\text{m}}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t - \theta - \phi) \] \[ \phi = \tan^{-1}\frac{\omega L}{R} \]ここで,$|Z| = \sqrt{R^2 + (\omega L)^2}$ とすれば,$|Z|$ は電圧と電流の大きさを関係づける量でインピーダンスという。
$RL$ 直列回路の電圧・電流波形
交流電源電圧源の大きさを 100 V(実効値),周波数を 60 Hz,抵抗 $R$ の大きさを 7.5 Ω,インダクタンス $L$ の大きさを 20 mH としたときの,電圧・電流波形を下図に示す。電流は電圧よりも遅れている(位相差は 0.788 [rad])ことがわかる。
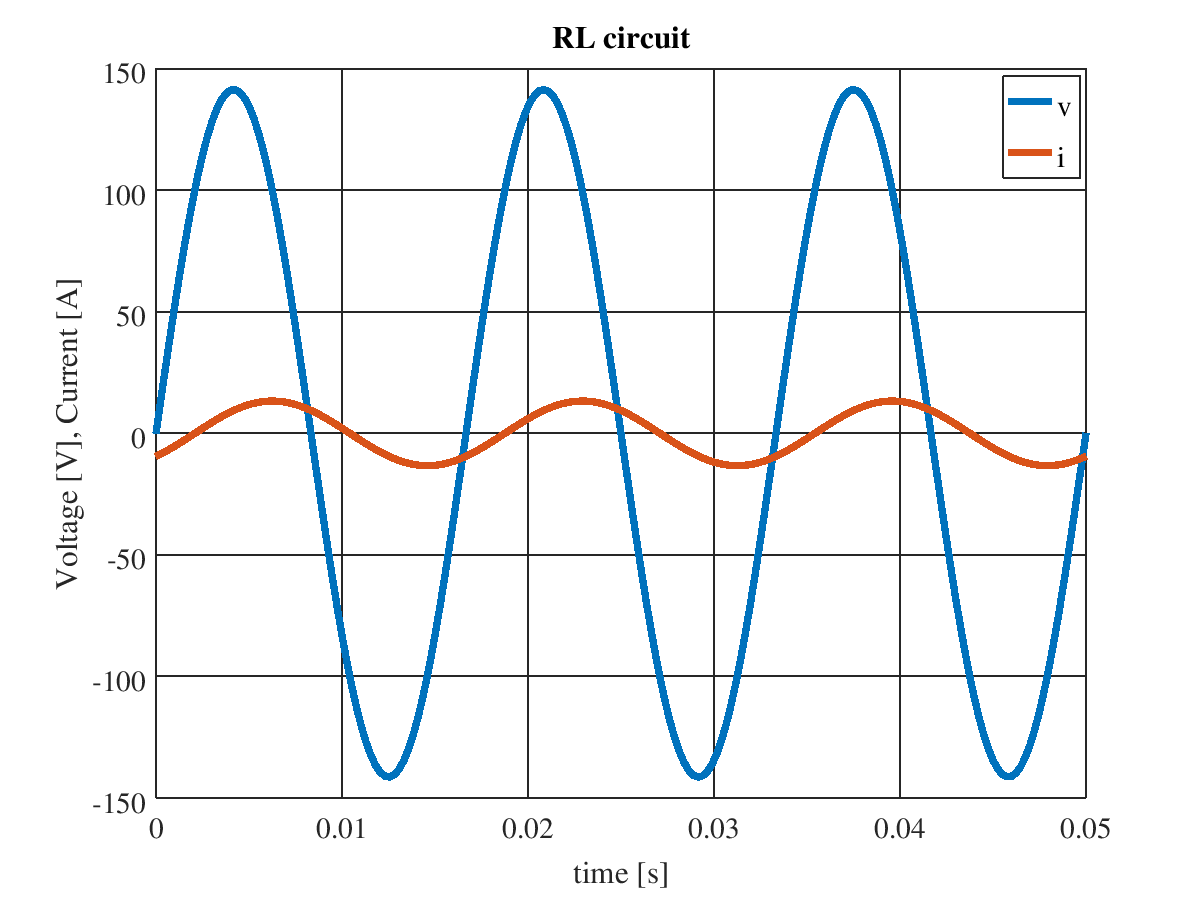
なお,インピーダンスと位相の大きさは,次式で求められる。
\[ |Z| = \sqrt{R^2 + (\omega L)^2}=\sqrt{7.5^2 + (2\pi \times 60 \times 0.020)^2}=10.6 \text{ [Ω]} \] \[ \phi = \tan^{-1}\frac{\omega L}{R} = \tan^{-1}\frac{2\pi \times 60 \times 0.020}{7.5}=0.788 \text{ [rad]} \]$RL$ 直列回路の力率
$RL$ 直列回路の力率は,次式で求められる。(ただし,インダクタンス $X$ [Ω] は,$X = \omega L$ である。)
\[ \frac{R}{\sqrt{R^2+(\omega L)^2}} \times 100 = \frac{100R}{\sqrt{R^2+X^2}} \]過去問題
- 2019年度 上期 No. 4 RL 直列回路
- 平成30年度(2018年度) 下期 No. 2 RL 直列回路
- 平成30年度(2018年度) 上期 No. 1 コイルに流れる電流
- 平成25年度(2013年度) 下期 No. 2 コイルに流れる電流
- 平成25年度(2013年度) 上期 No. 3 RL 直列回路の力率
$RC$ 直列回路
下図のように抵抗 $R$,キャパシタンス $C$ を直列に接続した回路に交流電源電圧 $e$ を加えたとき,電流 $i$ が流れたとすれば,次式が成り立つ。
\[ Ri + \frac{1}{C}\int i \text{d}t = e \]
$e = E_\text{m}\sin(\omega t - \theta)$ の交流電源電圧を加えたとすれば,瞬時電流 $i$ は次式となる。$\phi$ は,電圧,電流の位相差である。
\[ i = \frac{E_\text{m}}{\sqrt{R^2 + (-\frac{1}{\omega C})^2}} \sin(\omega t - \theta - \phi) \] \[ \phi = \tan^{-1}\frac{-\frac{1}{\omega C}}{R} \]ここで,$|Z| = \sqrt{R^2 + (-\frac{1}{\omega C})^2}$ とすれば,$|Z|$ は電圧と電流の大きさを関係づける量でインピーダンスという。
$RC$ 直列回路の電圧・電流波形
交流電源電圧源の大きさを 100 V(実効値),周波数を 60 Hz,抵抗 $R$ の大きさを 5 Ω,キャパシタンス $C$ の大きさを 500 μF としたときの,電圧・電流波形を下図に示す。電流は電圧よりも進んでいる(位相差は -0.815 [rad],進みを「-」で表現する)ことがわかる。
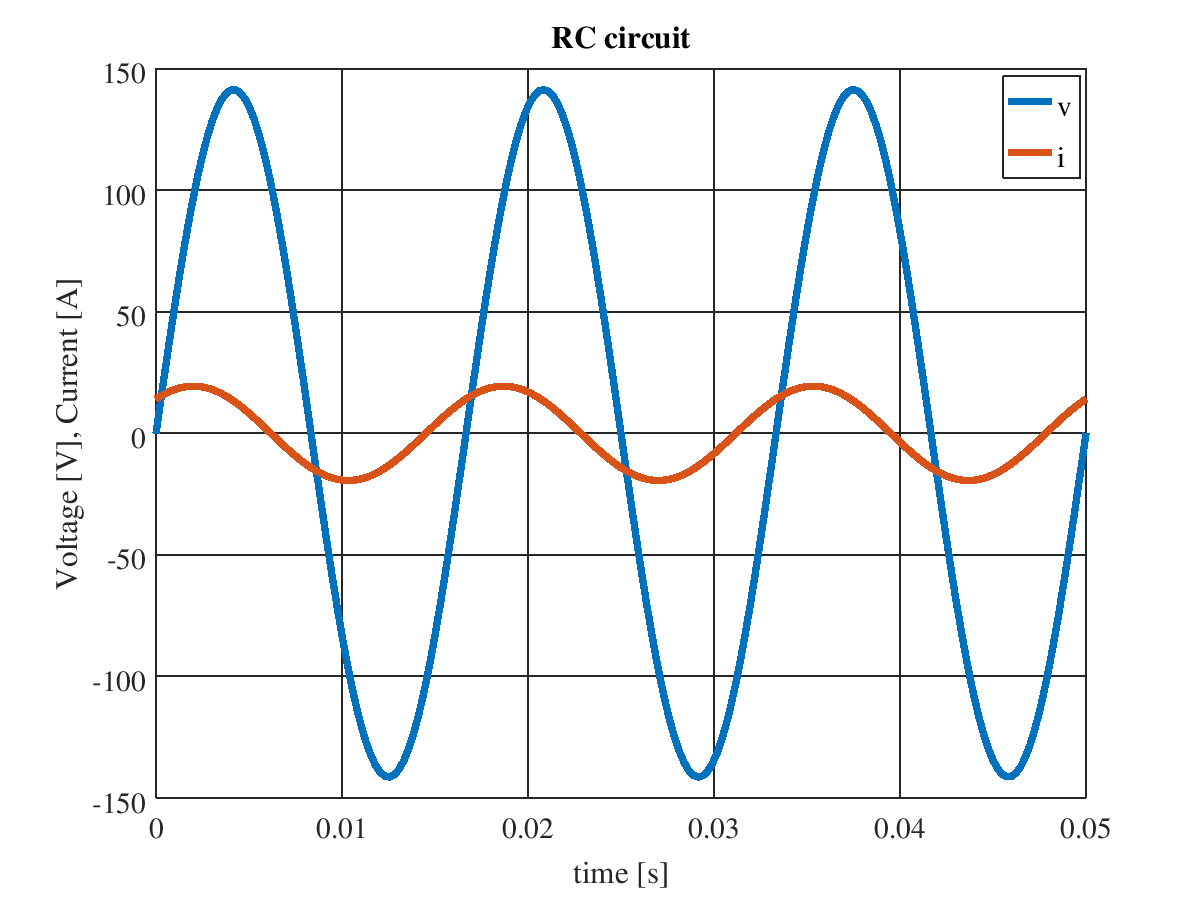
なお,インピーダンスと位相の大きさは,次式で求められる。
\[ |Z| = \sqrt{R^2 + (-\frac{1}{\omega C})^2}=\sqrt{5^2 + (-\frac{1}{2\pi\times60\times 500\times 10^{-6}})^2}=7.29 \text{ [Ω]} \] \[ \tan^{-1}\frac{-\frac{1}{\omega C}}{R}=\tan^{-1}\frac{-\frac{1}{2\pi\times60\times 500\times 10^{-6}}}{5}=-0.815 \text{ [rad]} \]過去問題
$LC$ 並列回路
$LC$ 並列回路を下図に示す。図において,$\dot{V}$ は交流電源電圧,$\dot{I_{C}}$ はコンデンサに流れる電流,$\dot{I_{L}}$ はインダクタンスに流れる電流である。
コンデンサに流れる電流 $\dot{I_{C}}$ は,交流電源電圧 $\dot{V}$ よりも 90 度進む。一方,インダクタンスに流れる電流 $\dot{I_{L}}$ は電圧 $\dot{V}$ よりも 90 度遅れる。
$LC$ 並列回路の左側に,電圧と電流のベクトルを示す。

LC 並列回路の電圧,電流波形を下図に示す。ただし,交流電源電圧 $\dot{V}$ の実効値は 100 V,周波数は 60 Hz,コンデンサに流れる電流 $\dot{I_C}$ の実効値は 60 A,インダクタンスに流れる電流 $\dot{I_L}$ の実効値は 80 A とした。
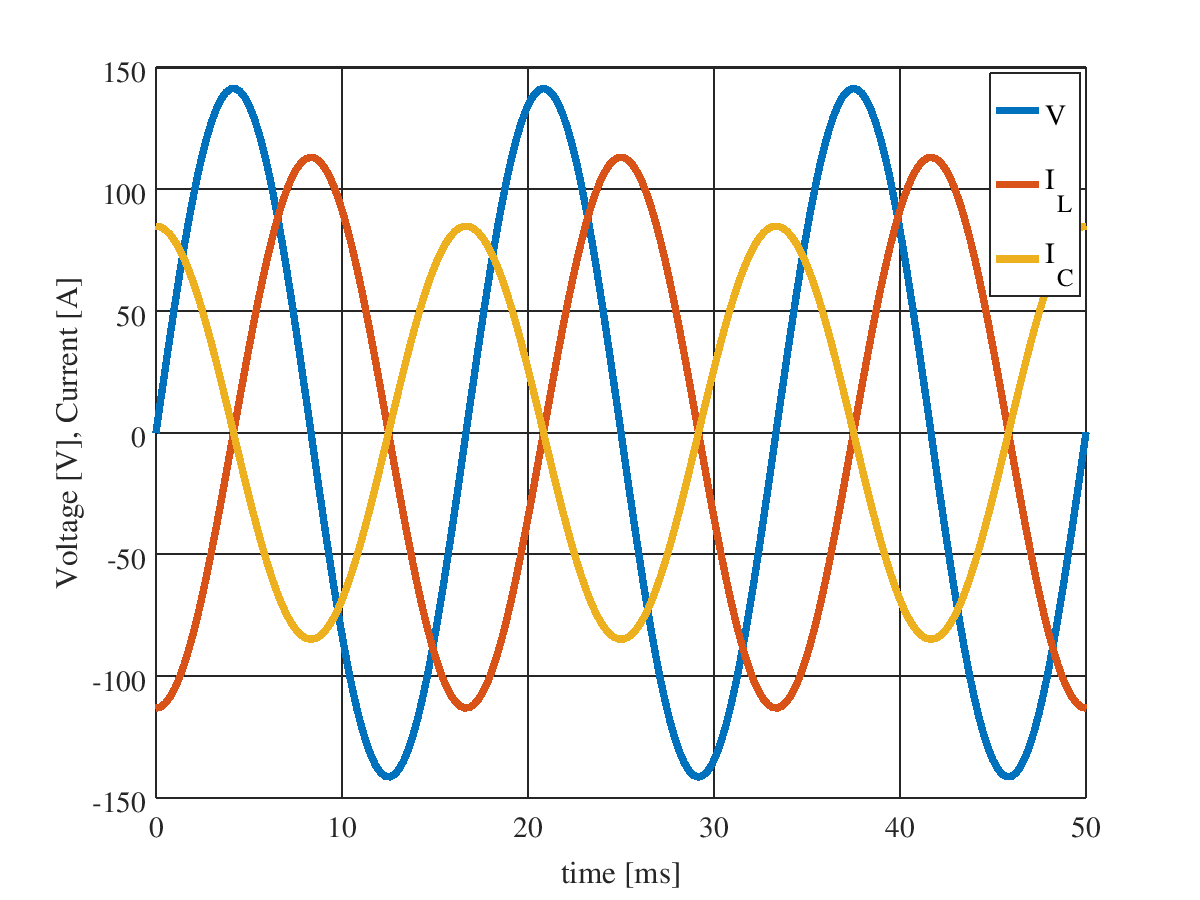
対称三相交流
対称三相交流における起電力の瞬時値は次のようになる。ただし,$E_\text{m}$ は振幅 [V],$\omega$ は角周波数 [rad/s] である。
\[ e_\text{a} = E_\text{m} \sin(\omega t) \] \[ e_\text{b} = E_\text{m} \sin(\omega t - \frac{2\pi}{3}) \] \[ e_\text{c} = E_\text{m} \sin(\omega t - \frac{4\pi}{3}) \]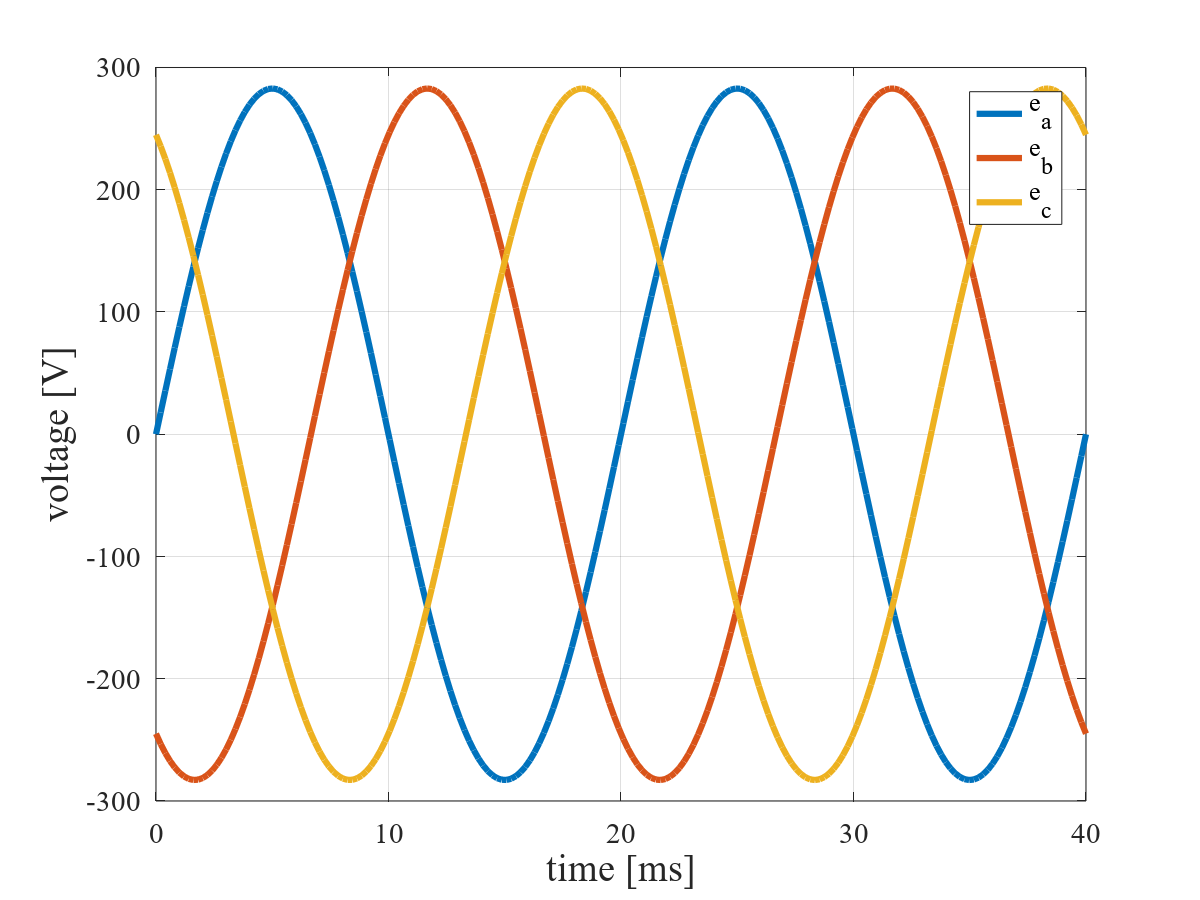
Y 結線(星形結線)
電源電圧を三つの抵抗 $R$ からなる Y 形負荷に接続する。線間電圧 $V_l$ と相電圧 $V_p$ の関係,線電流 $I_l$ と相電流 $I_p$ の関係は次式となる。
\[ V_l = \sqrt{3}V_p \] \[ I_l = I_p \]Y 結線(星形結線)では,線間電圧 $V_l$ は相電圧の $\sqrt{3}$ 倍,線電流 $I_l$ と相電流 $I_p$ は等しい。

例題
図のような三相 3 線式回路に流れる電流 $I$ [A] は。

解答・解説
Y 結線の線電流は相電流に等しい。よって,線電流 $I$ [A] は次式で求められる。
\[ I = \frac{200/\sqrt{3}}{10} = 11.6 \text{ [A]} \]よって,正解はロ.11.6である。
過去問題
- 2019年度 下期 No. 5 三相 3 線式回路(Y 結線)に流れる電流
- 平成30年度(2018年度) 下期 No. 5 三相 3 線式回路(Y 結線)に流れる電流
- 平成30年度(2018年度) 上期 No. 5 三相負荷(Y 結線)の線間電圧
- 平成25年度(2013年度) 上期 No. 5 三相 3 線式回路(Y 結線)の断線
デルタ結線(三角結線)
電源電圧を三つの抵抗 $R$ からなる Δ 形負荷に接続する。線間電圧 $V_l$ と相電圧 $V_p$ の関係,線電流 $I_l$ と相電流 $I_p$ の関係は次式となる。
\[ V_l = V_p \] \[ I_l = \sqrt{3}I_p \]デルタ結線(三角結線)では,線間電圧 $V_l$ と相電圧 $V_p$ は等しく,線電流 $I_l$ は相電流 $I_p$ の $\sqrt{3}$ 倍である。

過去問題
コンデンサによる力率改善
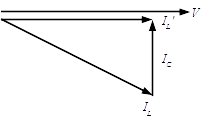
交流回路で,負荷に対してコンデンサ C を設置して,力率を改善できる。このときの電流計の指示値は,コンデンサ設置前と比べて減少する。

下図の $I_L$ はコンデンサ設置前の電流,$I_L'$ はコンデンサ設置後の電流である。
進相コンデンサ(容量 50 μF)の写真を下図に示す。

過去問題
電気回路の計算
オームの法則(Ohm's law)
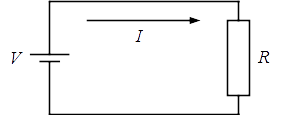
普通の抵抗素子では,オームの法則が成り立つ。
\[ V = RI \] \[ I = \frac{V}{R} \] \[ R =\frac{V}{I} \]抵抗 $R$ [Ω] は,抵抗に印加される電圧 $V$ [V] と,抵抗を流れる電流 $I$ [A] の比で表される。すなわち,電圧 $V$ は抵抗に注入された電流 $I$ に比例する。

ここに,比例定数 $R$ を電気抵抗または単に抵抗といい,単位としてオームが用いられ,記号 Ω で表される。抵抗 $R$ の逆数 $G = 1/R$ をコンダクタンスといい,単位としてジーメンスが用いられ,記号 S で表される。
過去問題
抵抗の直列接続(series connection)
抵抗を直列に接続したとき,全抵抗は各抵抗の和で表される。
\[ V = R_1 I + R_2 I = (R_1 + R_2)I = RI \] \[ R_1 + R_2 = R \]
抵抗の並列接続(parallel connection)
抵抗を並列に接続したとき,全抵抗の逆数は各抵抗の逆数の和で表される。
\[ I = \frac{V}{R} = \frac{1}{R} V \] \[ I_1 + I_2 = \frac{V}{R_1} + \frac{V}{R_2} = (\frac{1}{R_1} + \frac{1}{R_2})V \]$I = I_1 + I_2$ であるので,合成抵抗 $R$は次式となる。
\[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{R_1 + R_2}{R_1 R_2} \]
例題
図のような回路で,端子 a-b 間の合成抵抗 [Ω] は。

解答・解説
右上,3 Ω 2 個の抵抗を並列に接続した部分の合成抵抗は 1.5 Ω である。下辺,3 Ω 2 個の抵抗を直列に接続した部分の合成抵抗は 6 Ω である。端子 a - b 間の合成抵抗は,1.5 Ω と 6 Ω の抵抗を並列に接続したときの合成抵抗であり,解答はロ.1.2 Ω である。
過去問題
- 2019年度 下期 No. 1 回路の合成抵抗
- 2019年度 上期 No. 1 回路の電圧
- 平成30年度(2018年度) 下期 No. 1 合成抵抗
- 平成30年度(2018年度) 上期 No. 1 合成抵抗
ブリッジ回路の平衡条件
ブリッジ回路(bridge circuit)が平衡しているとき,検流計 G の指示値が 0 [A] となる。つまり,検流計両端の電位が等しく,次の二つ式が成り立つ。
\[ R_1 I_1 = R_2 I_2 \] \[ R_3 I_1 = R_4 I_2 \]すなわち,ブリッジ回路の平衡条件が成り立つとき,次の式が成り立つ。この式より,既知の三つの抵抗を用いて,未知の一つの抵抗の大きさを求めることができる。
\[ R_1 R_4 = R_2 R_3 \]
- 検流計とは,電流を検出し,測定するための機器である。
本稿の参考文献
- 一般財団法人 電気技術者試験センター,「第二種電気工事士学科試験 例題 1. 電気に関する基礎理論」
- 平山 博,大附 辰夫 著,「電気回路論[2 版改訂]」,電気学会
- 広瀬 敬一 原著,炭谷 英夫 著,「電気機器設計概論(4 版改定)――設計基礎から製図の基本まで――」,電気学会
- 電気事業講座編集幹事会 編纂,「電気事業講座 電気事業辞典」,エネルギーフォーラム,2008年6月10日 初版
- 国際度量衡局(BIPM),「国際単位系(SI)第 9 版(2019)日本語版」
- 臼田 孝,「国際単位系の全体像について」,電学誌,139巻6号,2019年
- 中村 秀司,「アンペアの定義改定と単電子素子」,電学誌,139巻6号,2019年