断面二次モーメント
はじめに
本稿では,断面二次モーメントについて説明したのち,様々な断面形状の断面二次モーメントを導出する。
目次
断面二次モーメントとは
曲げモーメントに対するはりの部材の変形のしにくさを表した量である。物体の断面(大きさや形状)を変えると,断面二次モーメント(area moment of inertia, 2nd moment of area, second area moment, quadratic moment of alea)の値も変化するので,設計上の指標として用いられる。
単純な形状のまっすぐなはりに曲げモーメントだけが作用する場合,はりには外力である曲げモーメントの大きさにつり合う曲げ応力が生じる。そして,はりの断面を見ると,中立面を挟んで曲がりの内側は圧縮応力(compressive stress),外側は引張応力(tensile stress)となる。

はりには曲げモーメントだけが作用しているので,力のつり合いを考えると,はりの断面 A-A' 全体について引張応力および圧縮応力を積分した値はゼロになる。また,はりの内部で圧縮応力と引張応力がゼロの面,すなわち伸びも縮みもしない面を中立面という。そして,中立面 N-N' と断面 A-A'(横断面)とが交わってできる線を中立軸(neutral axis)という。
中立丸軸や角形などの単純な形状において,中立軸は断面図形の図心(centroid of area)を通過する。
はりに生じる応力やたわみを求める場合,断面二次モーメントを計算する必要がある。上図のように,はりの断面の微小面積 $\text{d}A$ を考えると,中立軸まわりのモーメントは応力 $\sigma$,微小面積 $\text{d}A$,中立軸からの距離 $y$ の積になる。断面二次モーメントとは,ある断面における中立軸に関するモーメントの総和として定義される。
下図に示すような図形において,その重心 G を図心という。したがって,図のように図心 G を原点とする直角座標系 $(y,z)$ を考える。

断面の微小面積要素 $\text{d}A$ と微小要素の $z$ 軸から距離 $y$ とすると,$z$ 軸に関する断面二次モーメント $I_z$ は次式で求められる。
\[ I_z = \int_{A}{y^2}\text{d}A \]断面の微小面積要素 $\text{d}A$ と微小要素の $y$ 軸から距離 $z$ とすると,$y$ 軸に関する断面二次モーメント $I_y$ は次式で求められる。
\[ I_y = \int_{A}{z^2}\text{d}A \]なお,断面二次モーメントの量記号,次元,SI 単位は次表で表される。
| 項目 | 記号,次元,単位 | 説明 |
|---|---|---|
| 量記号 | $I$ | 大文字のアイ |
| 次元 | $L^4$ | 長さの 4 乗 |
| SI 単位 | m4 | メートルの 4 乗 |
(参考)バリニオンの定理
バリニオンの定理は「多くの平衡な力が作用するとき,それらの力による任意点まわりのそれぞれの力によるモーメントの総和は,これらの力の合力によるその点まわりのモーメントに等しい」である。
ピエール・ヴァリニョン
ピエール・ヴァリニョン(Pierre Varignon,1654 年 - 1722 年)はフランスの数学者である。静力学の分野でのヴァリニョンの定理(バリニオンの定理)で知られる。

(出典)フリー百科事典『ウィキペディア』
はりに荷重が加えられたとき,はりの断面には均一な垂直応力度が作用する。また,垂直応力度の合力が軸方向力である。軸方向力が作用する線は,材軸線と呼ばれ,構造力学では,構造物をこの線上に断面が集約されていると理想化して解析を行う。
(参考)断面一次モーメント
断面一次モーメントは断面の図心やせん断応力度を求めるときに使われる。
図心の定義より,次式が成り立つ。
\[ \int_{A}{y}\text{d}A=\int_{A}{z}\text{d}A=0 \]ここで,$A$ は図形の面積であり,各々の積分は $z$ 軸あるいは $y$ 軸に関する断面一次モーメント(geometrical moment of area)と呼ばれる。上式は図心を通る直交軸に関する断面一次モーメントは 0 となることを表している。
(参考)断面二次極モーメント
原点から微小面積 $\text{d}A$ までの距離を $r$ とすると,断面二次極モーメント(polar moment of inertia of area)$I_p$ は次式で求められる。
\[ I_p=\int_{A}{r^2}\text{d}A \]ここで,同じ原点からの $z$ 軸,$y$ 軸に関する断面二次モーメント $I_z$,$I_y$ を用いると,次式が成り立つ。
\[ I_p=I_z+I_y \]断面二次極モーメントは $z$ 軸および $y$ 軸に関する断面二次モーメントの和で表される。
図形を 90 度 回転させても同一の場合は,$I_z=I_y$ となり,次式が成り立つ。
\[ I_z=I_y=\frac{I_p}{2} \]はりの曲げ応力
はりの任意の断面にはせん断力と曲げモーメントが作用している。したがって,各断面にはせん断力につり合うようにせん断応力が生じ,また,曲げモーメントにつり合う垂直応力が生じる。一方,はりの軸線方向には荷重が作用しない場合を考えるから,断面に垂直な応力の軸方向の合力は 0 になる。
このように,曲げによって断面に垂直に生じ,その合力が 0 となる応力を曲げ応力(bending stress)という。曲げ応力は,「変形前に平面であった断面は変形後も軸線に垂直な平面を保つ」というベルヌーイ・ナビエ(Bernoulli-Navier)の仮定を基にして求めることができる。
ベルヌーイ・オイラーの仮定(Bernoulli-Euller's hypothesis)
はり理論は,中立軸に垂直な断面は,変形後においても平面を保ちかつ中立軸に垂直であるという仮定に基づいて理論が構築されている。これがはり理論の根幹となるべきベルヌーイ・オイラーの仮定であり,はりや板の古典理論は,この考え方に基づいて導かれている。板理論ではキルヒホッフの仮定,殻理論ではキルヒホッフ・ラブの仮定といわれている。
長方形断面の断面二次モーメント導出
図に示す幅 $B$,高さ $t$ の長方形断面の $y$ 軸に関する断面二次モーメント $I_z$ を求める。
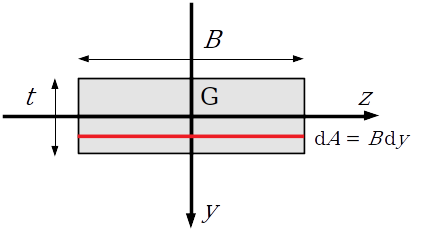
長方形の図心 G を通り,各辺に平行な座標系 $(y, z)$ を考えると,$z$ 軸から距離 $y$ の位置にある微小要素の面積は次式で求められる。
\[ \text{d}A = B \text{d}y \]$z$ 軸に関する対称性を考慮し,$y$ 軸に関する断面二次モーメント $I_z$ を求める。
\[ I_z = \int_{A} y^2 \text{d}A \] \[ I_z = 2\int^{\frac{t}{2}}_{0} y^2 \cdot B\text{d}y \] \[ I_z = 2B[\frac{y^3}{3}]^{\frac{t}{2}}_{0} \] \[ I_z = \frac{Bt^3}{12} \]$y$ 軸に関する断面二次モーメントは,幅 $B$ に比例し,高さ $t$ の 3 乗に比例する。$y$ 方向にたわみにくくするためには,幅 $B$ よりも高さ $t$ を大きくするほうが効果的であることがわかる。
一方,$y$ 軸から距離 $z$ の位置にある微小要素の面積は,$\text{d}A=t \text{d}z$ であるから,$z$ 軸に関する断面二次モーメント $I_y$ は次式で求められる。
\[ I_y = \int_{A}z^2 \text{d}A \] \[ I_y = 2\int^{\frac{B}{2}}_{0} z^2 \cdot t\text{d}z \] \[ I_y = 2t[\frac{z^3}{3}]^{\frac{B}{2}}_{0} \] \[ I_y = \frac{B^3 t}{12} \]正方形断面の断面二次モーメント
断面が正方形,つまり,$B=t$ のときの断面二次モーメント $I_z=I_y$ は次式で表される。
\[ I_z=I_y=\frac{B^4}{12} \]平鋼の断面二次モーメント
形状が単純に平たい帯状の鋼材である平鋼(FB,フラットバー)の断面二次モーメントを求める。なお,平鋼とは,長方形の断面に熱間圧延された鋼で,所定の長さに切断され,供給されるものをいう。
| $t$ [mm] | $B$ [mm] | $I_z$ [mm4] | $I_y$ [mm4] |
|---|---|---|---|
| 4.5 | 32 | 243 | 12,288 |
| 4.5 | 50 | 380 | 46,875 |
| 4.5 | 65 | 494 | 102,984 |
| 6 | 32 | 576 | 16,384 |
| 6 | 50 | 900 | 62,500 |
| 6 | 65 | 1,170 | 137,313 |
| 9 | 32 | 1,944 | 24,576 |
| 9 | 50 | 3,038 | 93,750 |
| 9 | 65 | 3,949 | 205,969 |
H 形断面の断面二次モーメント導出
下図に示すウェブの幅 $t_1$,フランジの幅 $B$,フランジ厚さ $t_2$,高さ $H$ の H 形断面(H-beam)の $y$ 軸に関する断面二次モーメント $I_z$ を求める。
H 形鋼は,断面がローマ字の「H」形の形鋼である。様々な所に使われている代表的な形鋼である。他の形鋼に比べて,断面効率(重量当たりの曲げ剛性や曲げ強度)が優れている。

ウェブ部($\displaystyle 0 \le y \le \frac{t_1}{2}$)
ウェブ部の微小要素の面積 $\text{d}A$ は次式で表される。
\[ \text{d}A=H\text{d}y \]ウェブ部以外($\displaystyle \frac{t_1}{2} \le y \le \frac{B}{2}$)
ウェブ部以外の微小要素の面積 $\text{d}A$ は次式で表される。
\[ \text{d}A=2t_2 \text{d}y \]$y$ 軸に関する断面二次モーメント $I_z$
H 形断面の図心 G を通り,各辺に平行な座標系 $(y, z)$ を考える。$z$ 軸に関する対称性を考慮し,$y$ 軸に関する断面二次モーメント $I_z$ を求める。
\[ I_z = \int_A y^2 \text{d}A \] \[ I_z = 2\int^{\frac{t_1}{2}}_{0} y^2 \cdot H\text{d}y + 2\int^{\frac{B}{2}}_{\frac{t_1}{2}} y^2 \cdot 2t_2 \text{d}y \] \[ I_z = 2H\int^{\frac{t_1}{2}}_{0} y^2 \text{d}y + 4t_2\int^{\frac{B}{2}}_{\frac{t_1}{2}} y^2 \text{d}y \] \[ I_z = 2H[\frac{y^3}{3}]^{\frac{t_1}{2}}_{0} + 4t_2[\frac{y^3}{3}]^{\frac{B}{2}}_{\frac{t_1}{2}} \] \[ I_z = \frac{{t_1}^3 H}{12}+\frac{t_2 B^3}{6} -\frac{{t_1}^3 t_2}{6} \] \[ I_z = \frac{2t_2 B^3 + {t_1}^3(H-2t_2)}{12} \](参考)ウェブとフランジについて
ウェブとフランジについて説明する。
- ウェブ(web)
- フランジで挟まれる板をウェブと呼ぶ。ウェブではせん断力を負担する。
- フランジ(flange)
- はりに用いられる部材では上縁あるいは下縁に板状の部材を設けることがあり,これについてフランジと呼ぶ。フランジを設けることで断面二次モーメントが大きくなり,曲げ剛性が向上する。
例として,H-125 × 60 × 60 × 6 × 8 において,ウェブの有無での断面二次モーメントを比較する。ウェブの有無で,断面二次モーメントはほとんど変わらないことがわかる。
| ウェブあり | ウェブなし | |
|---|---|---|
| 断面二次モーメント $I_z$ [mm4] | 289,962 (100 %) |
287,712 (99.22 %) |
I 形断面の断面二次モーメント導出
下図に示すウェブの幅 $t_1$,フランジの幅 $B$,フランジ厚さ $t_2$,高さ $H$ の I 形断面(I-beam)の $y$ 軸に関する断面二次モーメント $I_z$ を求める。
I 形鋼とは,断面がローマ字の「I」の形をした形鋼である。形状的には H 形鋼に近いが,同一サイズでは H 形鋼と比べて板厚が厚く,重量,剛性ともに大きい。フランジ内面にはテーパー(傾斜)がつけられている。I 型ジョイスト,アイビームとも呼ばれる。

ウェブ部($\displaystyle 0 \le y \le \frac{H}{2}-t_2$)
ウェブ部の微小要素の面積 $\text{d}A$ は次式で表される。
\[ \text{d}A=t_1 \text{d}y \]フランジ部($\displaystyle \frac{H}{2}-t_2 \le y \le \frac{H}{2}$)
フランジ部の微小要素の面積 $\text{d}A$ は次式で表される。
\[ \text{d}A=B \text{d}y \]$y$ 軸に関する断面二次モーメント $I_z$
I 形断面の図心 G を通り,各辺に平行な座標系 $(y, z)$ を考える。$z$ 軸に関する対称性を考慮し,$y$ 軸に関する断面二次モーメント $I_z$ を求める。
\[ I_z=\int_A y^2 \text{d}A \] \[ I_z=2\int^{\frac{H}{2}-t_2}_{0} y^2 \cdot t_1 \text{d}y +2\int^{\frac{H}{2}}_{\frac{H}{2}-t_2} y^2 \cdot B\text{d}y \] \[ I_z=2t_1[\frac{y^3}{3}]^{\frac{H}{2}-t_2}_{0} +2B[\frac{y^3}{3}]^{\frac{H}{2}}_{\frac{H}{2}-t_2} \] \[ I_z=2t_1 \times \frac{1}{3}\times(\frac{H}{2}-t_2)^3 +2B \times \frac{1}{3}\times(\frac{H}{2})^3 -2B \times \frac{1}{3}\times(\frac{H}{2}-t_2)^3 \] \[ I_z=\frac{t_1}{12}(H-2t_2)^3+\frac{BH^3}{12} -\frac{B}{12}(H-2t_2)^3 \] \[ I_z=\frac{BH^3-(H-2t_2)^3(B-t_1)}{12} \]円形断面の断面二次モーメント導出
図に示す直径が $d$ である円形(中実丸棒)断面の $y$ 軸に関する断面二次モーメント $I_z$ を求める。

赤色で示した微小要素の面積 $\text{d}A$ は次式で表される。
\[ \text{d}A = 2 \sqrt{\frac{d^2}{4}-y^2}\cdot \text{d}y \]円形断面の $y$ 軸に関する断面二次モーメント $I_z$ は次式で求められる。
\[ I_z=\int_{A} y^2 \text{d}A=\int^{\frac{d}{2}}_{-\frac{d}{2}} y^2 \cdot 2 \sqrt{\frac{d^2}{4}-y^2}\cdot \text{d}y \]ここで,$\displaystyle y=\frac{d}{2}\sin{\theta}$ とおく。
\[ \frac{\text{d}y}{\text{d}\theta}=\frac{d}{2}\cos{\theta} \] \[ \text{d}y=\frac{d}{2}\cos{\theta} \text{d}\theta \]| $y$ | $\displaystyle -\frac{d}{2}$ | 0 | $\displaystyle \frac{d}{2}$ |
|---|---|---|---|
| $\theta$ | $\displaystyle -\frac{\pi}{2}$ | 0 | $\displaystyle \frac{\pi}{2}$ |
断面二次モーメント $I_z$ は,次式のように変形できる。
\[ I_z=\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \frac{d^2}{4} \sin^2 \theta \cdot 2 \cdot \sqrt{\frac{d^2}{4}-\frac{d^2}{4}\sin^2 \theta} \cdot \frac{d}{2}\cos\theta \cdot \text{d}\theta \] \[ I_z=\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \frac{d^2}{4} \sin^2 \theta \cdot 2 \cdot \frac{d}{2}\cos\theta \cdot \frac{d}{2}\cos\theta \cdot \text{d}\theta \] \[ I_z=\frac{d^4}{8}\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \sin^2{\theta}\cos^2{\theta} \text{d}\theta \]ここで,倍角の公式 $\sin{2\theta}=2\sin{\theta}\cos{\theta}$ より,次式に変形する。
\[ I_z=\frac{d^4}{32}\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \sin^2{2\theta} \text{d}\theta \]ここで,半角の公式 $\displaystyle \sin^2{\frac{\theta}{2}}=\frac{1-\cos{\theta}}{2}$ より,次式に変形する。
\[ I_z=\frac{d^4}{32}\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \frac{1-\cos{4\theta}}{2} \text{d}\theta \] \[ I_z=\frac{d^4}{32}[\frac{\theta}{2}-\frac{\sin{4\theta}}{8}]^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \] \[ I_z=\frac{\pi d^4}{64} \]別解 断面二次極モーメントによる導出
断面二次極モーメント $I_p$により,断面二次モーメント $I_z$ を導出する。

上図に示す図心 G から距離 $r$ の微小円輪要素の面積 $\text{d}A$ は,次式で求められる。
\[ \text{d}A=2\pi r \cdot \text{d}r \]断面二次極モーメント $I_p$ を求める。
\[ I_p=\int_{A}r^2 \text{d}A \] \[ I_p=\int^{\frac{d}{2}}_{0}r^2 \cdot 2\pi r \cdot \text{d}r \] \[ I_p=2\pi\int^{\frac{d}{2}}_{0} r^3 \text{d}r \] \[ I_p=2\pi[\frac{r^4}{4}]^{\frac{d}{2}}_{0} \] \[ I_p=\frac{\pi d^4}{32} \]図形の対称性より,$I_z = I_y$ であるので,円形断面の $y$ 軸に関する断面二次モーメント $I_z$ は,次式で求められる。
\[ I_z =\frac{I_p}{2}=\frac{\pi d^4}{64} \]中空円形断面の断面二次モーメント導出
図に示す外径が $D$,内径が $d$ である中空円形(中空丸棒)断面の $y$ 軸に関する断面二次モーメント $I_z$ を求める。なお,断面二次極モーメント $I_p$により,断面二次モーメント $I_z$ を導出する。

上図に示す図心 G から距離 $r$ の微小円輪要素の面積 $\text{d}A$ は,次式で求められる。
\[ \text{d}=2\pi r \cdot \text{d}r \]断面二次極モーメント $I_p$ を求める。
\[ I_p=\int_{A}r^2 \text{d}A \] \[ I_p=\int^{\frac{D}{2}}_{\frac{d}{2}}r^2 \cdot 2\pi r \cdot \text{d}r \] \[ I_p=2\pi\int^{\frac{D}{2}}_{\frac{d}{2}} r^3 \text{d}r \] \[ I_p=2\pi[\frac{r^4}{4}]^{\frac{D}{2}}_{\frac{d}{2}} \] \[ I_p=\frac{\pi (D^4-d^4)}{32} \]図形の対称性より,$I_z = I_y$ であるので,円形断面の $y$ 軸に関する断面二次モーメント $I_z$ は,次式で求められる。
\[ I_z =\frac{I_p}{2}=\frac{\pi (D^4-d^4)}{64} \]長方形管断面の断面二次モーメント導出
図に示す幅 $b$,内幅 $b_1$,高さ $h$,内高さ $h_1$ の長方形管断面の $y$ 軸に関する断面二次モーメント $I_z$ を求める。長方形管は,中空長方形,角パイプともいう。

長方形管の図心 G を通り,各辺に平行な座標系 $(y, z)$ を考える。$z$ 軸に関する対称性を考慮し,また $0 \le y \le h_1/2$ と $h_1/2 \le y \le h/2$ における微小要素の面積 $\text{d}A_1$,$\text{d}A_2$ はそれぞれ $(b-b_1) \text{d}y$ および $b \text{d}y$ であるから,$y$ 軸に関する断面二次モーメントは次式で求められる。
\[ I_z = \int_{A}y^2 \text{d}A \] \[ I_z = 2 \int^{h_1/2}_{0} (b-b_1)y^2 \text{d}y + 2 \int^{h/2}_{h_1/2} by^2 \text{d}y \] \[ I_z = 2(b-b_1)[\frac{y^3}{3}]^{h_1/2}_{0} + 2b[\frac{y^3}{3}]^{h/2}_{h_1/2} \] \[ I_z = \frac{b{h_1}^3}{12} - \frac{b_1{h_1}^3}{12} + \frac{bh^3}{12} - \frac{b{h_1}^3}{12} \] \[ I_z = \frac{bh^3-b_1h_1^3}{12} \]正方形管断面の断面二次モーメント
断面が正方形管,つまり,$b=h$,$b_1 = h_1$ のときの断面二次モーメント $I_z$ は次式で表される。
\[ I_z=I_y=\frac{b^4-{b_1}^4}{12} \]演習問題
断面二次モーメントに関する演習問題を示す。
図心の座標
図のような断面において,図心の座標 ($x_0$, $y_0$) の値を求めよ。ただし,$\displaystyle x_0 = \frac{S_y}{A}$,$\displaystyle y_0 = \frac{S_x}{A}$ であり,$S_x$,$S_y$ はそれぞれ $X$ 軸,$Y$ 軸まわりの断面一次モーメント,$A$ は全断面積を示すものとする。(単位は mm とする。)

図心を求めるために,下の図のように断面積が等しくなるよう 2 つに分けて考える。

断面 A の図心の座標は (10, 20),断面 B の図心の座標は (20, 50) である。よって,求める図心の座標は (15, 35) である。
別解
$X$ 軸まわりの断面一次モーメントは,次式で求められる。
\[ S_x=\int_A{y}\text{d}A=20\int_{0}^{40}{y}\text{d}y + 40\int_{40}^{60}{y}\text{d}y=56000 \]$Y$ 軸まわりの断面一次モーメントは,次式で求められる。
\[ S_y=\int_A{x}\text{d}A=60\int_{0}^{20}{x}\text{d}x+20\int_{20}^{40}{x}\text{d}x=24000 \]全断面積 $A$ は,次式で求められる。(断面 A と断面 B の断面積の和)
\[ A=40\times20+20\times40=1600 \]よって,図心の座標は,次式で求められる。
\[ x_0=\frac{S_y}{A}=\frac{24000}{1600}=15 \text{ [mm]} \] \[ y_0=\frac{S_x}{A}=\frac{56000}{1600}=35 \text{ [mm]} \]H 形断面と I 形断面の比較
図のような形状の等しい断面 A 及び断面 B において,図心を通る $X$ 軸に関する断面二次モーメントを求めよ。ただし,小数点以下は四捨五入とする。(単位は cm とする。)


H 形の断面 A の断面二次モーメントは,次式で求められ,337 [cm4] である。
\[ I_z = \frac{2t_2 B^3 + {t_1}^3(H-2t_2)}{12} = \frac{2 \times 2 \times 10^3 + 2^3(10-2\times 2)}{12}=337.3 \]I 形の断面 B の断面二次モーメントは,次式で求められ,689 [cm4] である。
\[ I_z=\frac{BH^3-(H-2t_2)^3(B-t_1)}{12}=\frac{10\times10^3-(10-2\times2)^3(10-2)}{12}=689.3 \]与えられた形状においては,H 形に比べ,I 形の方が断面二次モーメントが大きくなる。
本稿の参考文献
- The Free Encyclopedia WIKIPEDIA, "Second moment of area"
- JIS G 3192 : 2014『熱間圧延形鋼の形状,寸法,質量及びその許容差』,Dimensions, mass and permissible variations of hot rolled steel sections
- 機械工学辞典 Mechanical Engineering Dictionary