等分布荷重と集中荷重を受ける単純支持はり
はじめに
集中荷重を受ける単純梁を,等分布荷重を受けるように荷重条件のみ変更した場合に生じる変化について,解説する。なお,検討において,梁の自重を無視するものとする。
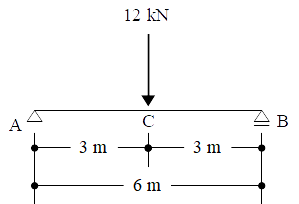
集中荷重 12 kN を受ける長さ 6 m の単純梁を下図に示す。集中荷重は梁の中央 C 点で受けるものとする。
等分布荷重 2 kN/m を受ける長さ 6 m の単純梁を下図に示す。

支点 A 及び 支点 B の反力
単純梁の視点 A の反力 $R_\text{A}$ [kN] と支点 B の反力 $R_\text{B}$ [kN] の和は,単純梁に作用する全荷重とつり合う。集中荷重,等分布荷重いずれも単純梁が受ける全荷重は 12 [kN] であり,支点 A 及び B の反力は,荷重条件変更後も,変わらない。
\[ R_\text{A}=R_\text{B}= 6 \text{ [kN]} \]最大せん断力
集中荷重を受ける単純梁の最大せん断力は,次式で求められる。
\[ Q_\text{max}=\frac{6-3}{6}\times12=6 \text{ [kN]} \]等分布荷重 $w$ [kN/m] を受ける長さが $l$ [m] の単純梁の最大せん断力は,次式で求められる。
\[ Q_\text{max}=\frac{wl}{2}=\frac{2 \times 6}{2}=6 \text{ [kN]} \]よって,最大せん断力は,荷重条件変更後も,変わらない。
せん断力図(SFD)
集中荷重を受ける単純梁と等分布荷重を受ける単純梁のせん断力図(SFD : Shearing Force Diagram)を示す。集中荷重は青線,分布荷重は赤線でせん断力図を示す。
最大せん断力の大きさは,集中荷重,等分布荷重いずれも 6 [kN] である。

最大曲げモーメント
集中荷重を受ける単純梁の最大曲げモーメントは,次式で求められる。
\[ M_\text{max}=\frac{3\times3}{6}\times 12=18 \]等分布荷重 $w$ [kN/m] を受ける単純梁の最大曲げモーメントは,次式で求められる。
\[ M_\text{max}=\frac{wl^2}{8}=\frac{2\times6^2}{8}=9 \]よって,最大曲げモーメントは,荷重条件変更後に,小さくなる。
曲げモーメント図(BMD)
集中荷重を受ける単純梁と等分布荷重を受ける単純梁の曲げモーメント図(BMD : Bending Moment Diagram)を示す。集中荷重は青線,分布荷重は赤線で曲げモーメント図を示す。
集中荷重の曲げモーメント最大値は 18 [kN·m],等分布荷重の曲げモーメント最大値は 9 [kN·m] である。

C 点におけるたわみ
縦弾性係数を $E$,梁の断面二次モーメントを $I_z$ として,C 点におけるたわみ $y$ を求める。
集中荷重 $P$ [kN] を受ける単純梁の C 点におけるたわみは,次式で求められる。
\[ y=\frac{Pl^3}{48EI_z}=\frac{12\times 6^3}{48EI_z}=\frac{54}{EI_z} \]等分布荷重 $w$ [kN/m] を受ける長さが $l$ [m] の単純梁のたわみ $y$ は,次式で求められる。
\[ y=\frac{5wl^4}{384EI_z}=\frac{5\times 2 \times 6^4}{384EI_z}=\frac{33.75}{EI_z} \]たわみ曲線
集中荷重を受ける単純梁と等分布荷重を受ける単純梁のたわみ曲線を示す。ただし,縦弾性係数を 1 [kN/m],断面二次モーメントを 1 [m4] とし,集中荷重は青線,分布荷重は赤線でたわみ曲線を示す。
集中荷重のたわみは 54 [m],等分布荷重のたわみは 33.75 [m] となる。
