集中荷重を受ける単純支持はりのたわみ
はじめに
集中荷重を受ける単純支持はりのせん断力,曲げモーメントおよびたわみをわかりやすく,そして詳細に計算する。

目次
検討モデル
集中荷重(concentrated load)による単純支持はり(simply supported beam)のせん断力(shearing force),曲げモーメント(bending moment)およびたわみ(deflection)を検討するモデルを図 1 に示す。

単純支持はりの支点 A は回転はできるが移動できない回転支点(hinged support),支点 B は回転と共に一方に移動できる移動支点(movable support)である。
単純支持はりの支点 A を $xy$ 座標の原点とし,原点より支点 B 方向を $x$ の正,原点より鉛直下向きを $y$ の正とする。また,単純支持はりの長さ(支点 A と 支点 B との間の距離)は $l$ とする。
単純支持はりの $x = a$ において作用する集中荷重 $P$ を想定する。
用語の説明
- 曲げ荷重(bending load)
- 支持されたはりを曲げるように作用する荷重
- 集中荷重(concentrated load)
- 1 点に集中して作用する荷重。ピンやボルトで付加されている状態や鋭いエッジで接触している場合などを表す。また,接触面自体は広くても,はり全体の長さから見ると十分に小さい接触領域の場合も近似的に集中荷重とみなす。
- たわみ(deflection)
- 部材が外力などの作用によってわん曲したとき,荷重を受ける前の材軸線と直角方向の変位量
反力(reaction force)と全荷重のつり合い
単純支持はりの支点 A における反力 $R_A$ と支点 B における反力 $R_B$ の和は,集中荷重 $P$ とつり合う。
\[ R_A + R_B = P \]一方,支点を A 点としたとき,B 点でのモーメントのつり合いは次式で表される。
\[ Pa - R_B l = 0 \]以上の 2 式より,単純支持はりの支点 A における反力 $R_A$ と支点 B における反力 $R_B$ は次式で表される。
\[ R_A = \frac{b}{l}P = \frac{l-a}{l}P \] \[ R_B = \frac{a}{l}P \]せん断力(shearing force)と曲げモーメント(bending moment)
集中荷重を受ける単純支持はりの支点 A から,$x$ の位置で切断したとき,切断面に作用するせん断力 $Q$ と曲げモーメント $M$ のイメージを図 2 に示す。

$0 ≤ x < a$ のとき
単純支持はりの支点 A における反力 $R_A$ だけを考慮すればよいので,せん断力と曲げモーメントは次式となる。
\[ Q = R_A = \frac{b}{l}P = \frac{l-a}{l}P \] \[ M = R_A x = \frac{b}{l}Px = \frac{l-a}{l}Px \]$a < x ≤ l$ のとき
単純支持はりの支点 A における反力 $R_A$ と集中荷重 $P$を考慮し,せん断力と曲げモーメントは次式となる。
\[ Q = R_A - P = \frac{b}{l}P - \frac{a + b}{l}P = -\frac{a}{l}P \] \[ M = R_A x - P(x-a)= \frac{a}{l}(l-x)P \]せん断力は,$a < x ≤ l$ のときは正の値,$a < x ≤ l$ のときは負の値となる。
曲げモーメントは,$a < x ≤ l$ のときは単純増加する一次関数,$a < x ≤ l$ のときは単純減少する一次関数で表される。また,最大曲げモーメント $M_{\text{MAX}}$ は,荷重点($x=a$)に生じ,大きさは次式となる。
\[ M_{\text{MAX}} = \frac{ab}{l}P = \frac{a(l-a)}{l}P \]せん断力図(SFD)
$P$ = 50 [N],$l$ = 1,000 [mm],$a$ = 600 [mm]($b$ = 400 [mm])としたとき,せん断力図(SFD:Shearing Force Diagram)を図 3 に示す。集中荷重を受ける単純支持はりのせん断力は,単純支持はりの左端($x = 0$)から荷重点($x=a$)までは正の値,荷重点($x=a$)から単純支持はりの右端($x=l$)までは負の値となる。そして,荷重点($x = a$)において,せん断力は正(+20 [N])から負(-30 [N])へ転じている。
$0 ≤ x < a$ のせん断力
\[ Q = \frac{b}{l}P = \frac{400}{1000} \times 50 = 20 \text{ [N]} \]$a < x ≤ l$ のせん断力
\[ Q = -\frac{a}{l}P = -\frac{600}{1000} \times 50 = -30 \text{ [N]} \]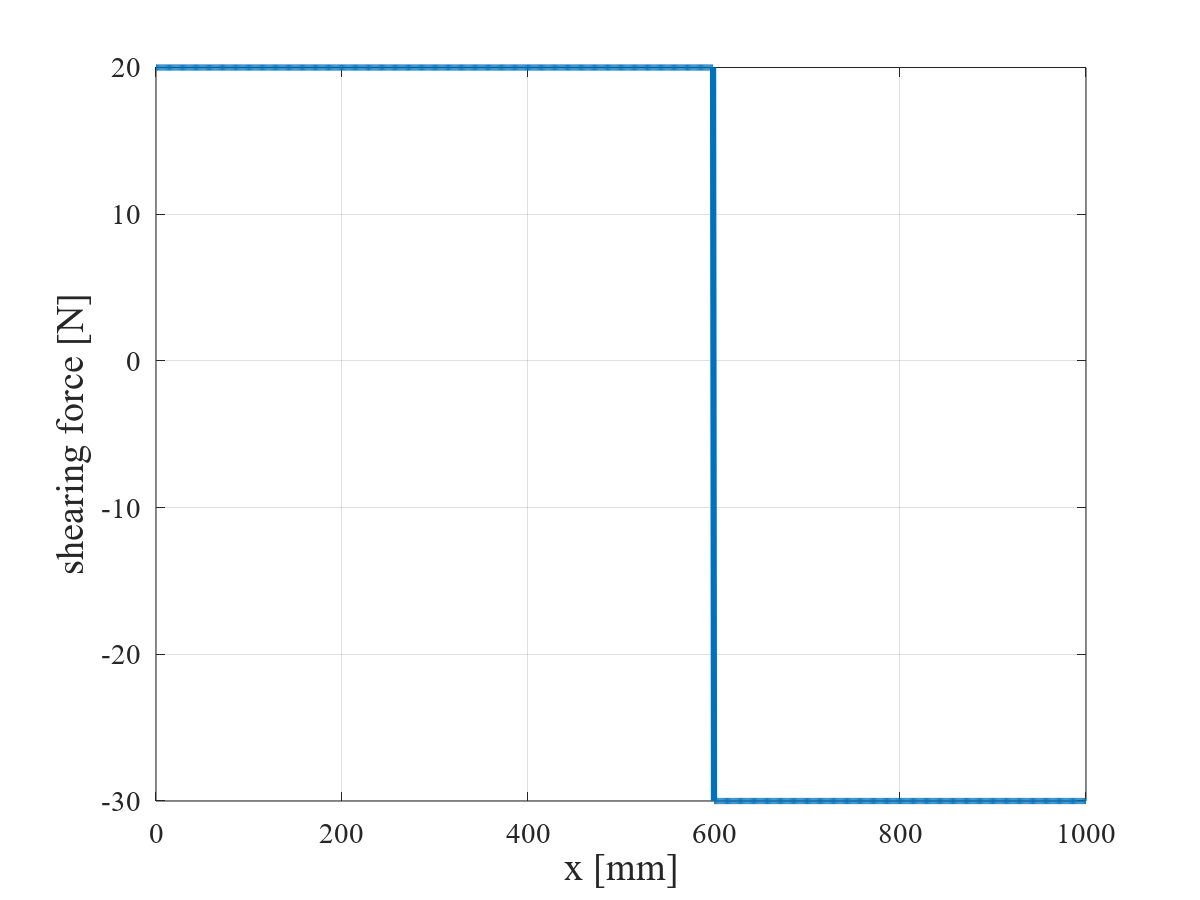
曲げモーメント図(BMD)
$P$ = 50 [N],$l$ = 1,000 [mm],$a$ = 600 [mm]($b$ = 400 [mm])としたときの,曲げモーメント図(BMD:Bending Moment Diagram)を図 4 に示す。集中荷重を受ける単純支持はりの曲げモーメントは,単純支持はりの左端($x = 0$)から荷重点($x=a$)までは単純増加する一次関数,荷重点($x=a$)から単純支持はりの右端($x=l$)までは単純減少する一次関数で表される。最大曲げモーメント $M_{\text{MAX}}$ は,荷重点($x=a$)に生じ,その大きさは 12,000 [N·mm] である。
\[ M_{\text{MAX}} = \frac{ab}{l}P = \frac{600 \times 400}{1000} \times 50 = 12,000 \text{ [N·mm]} \]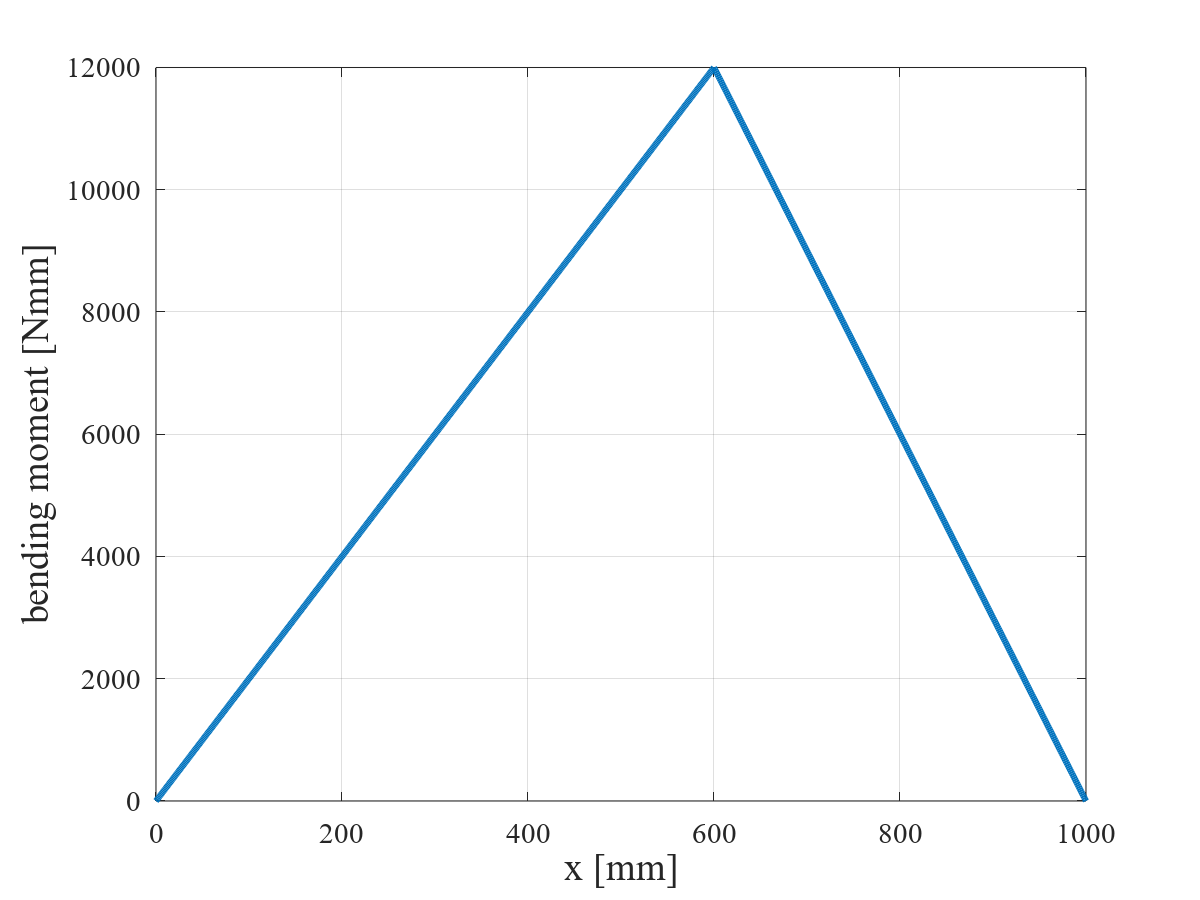
たわみ(deflection)
単純支持はりの支点 A から 距離 $x$ におけるたわみ $y(x)$ に関する微分方程式は,次式で与えられる。この式は,弾性曲線方程式(elastic curve equation)である。
$0 ≤ x < a$
\[ \frac{\text{d}^2 y(x)}{\text{d}x^2} = -\frac{M}{EI_z} = -\frac{P}{EI_z l}\frac{b}{l}x \]$a < x ≤ l$
\[ \frac{\text{d}^2 y(x)}{\text{d}x^2} = -\frac{M}{EI_z} = -\frac{P}{EI_z l}\frac{a}{l}(l-a) \]ここで,$E$ は縦弾性係数(modulus of longitudinal elasticity)またはヤング率(Young's modulus),$I_z$ ははりの横断面の $z$ 軸に関する断面二次モーメント(moment of inertia of area)である。すなわち,この微分方程式は,「たわみの 2 階微分が曲げモーメントを剛性($EI_z$)で割ったものを負にしたものに等しい」ことを意味する。
単純支持はりの場合,はりを固定する支点は変位しないと考えるため,弾性曲線はたわみ曲線(deflection curve equation)と一致する。
たわみ曲線の微分方程式を順次 $x$(断面の位置)で積分し,たわみ $y$ を求める。
$0 ≤ x < a$
\[ \frac{\text{d}y(x)}{\text{d}x} = -\frac{Pb}{EI_z l}(\frac{x^2}{2} + C_1) \]$a < x ≤ l$
\[ \frac{\text{d}y(x)}{\text{d}x} = -\frac{Pa}{EI_z l}\{-\frac{(l-x)^2}{2} + C_2\} \]$0 ≤ x < a$
\[ y(x) = -\frac{Pb}{EI_z l}(\frac{x^3}{6} + C_1 x + C_3) \]$a < x ≤ l$
\[ y(x) = -\frac{Pa}{EI_z l}\{\frac{(l-x)^3}{6} - C_2 (l-x) + C_4\} \]ここで,$C_1$,$C_2$,$C_3$,$C_4$は積分定数であり,はりの境界条件(boundary condition)から決定される。まず,$x = 0$ において$y = 0$,$x = l$ において$y=0$の境界条件より $C_3$,$C_4$を求める。
\[ C_3 = C_4 = 0 \]また,$x = a$ においてたわみ曲線は連続していなければならないから,$x = a$ の左右におけるたわみ角(すなわち $\displaystyle \frac{\text{d}y}{\text{d}x}$)およびたわみ(すなわち $y$)が等しくなる。これらの条件より,次式を得る。
\[ \frac{a^2 b}{2} + C_1 b = -\frac{a b^2}{2} + C_2 a \] \[ \frac{a^2}{6} + C_1 = \frac{b^2}{6} - C_2 \]これらの式より,$C_1$,$C_2$ を求める。
\[ C_1 = -\frac{a(a+2b)}{6} \] \[ C_2 = \frac{b(2a+b)}{6} \]したがって,支点 A から 距離 $x$ におけるたわみ $y(x)$ は次式となる。
$0 ≤ x < a$ のたわみ
\[ y(x) = \frac{Pb}{6EI_z l}\{-x^3 + a(a+2b)x\} \]$a < x ≤ l$ のたわみ
\[ y(x) = \frac{Pa}{6EI_z l}\{-(l-x)^3 + b(2a+b) (l-x)\} \]このようにしてはりのたわみを求める方法を重複積分法(double-integration method)という。
たわみ曲線(deflection curve)
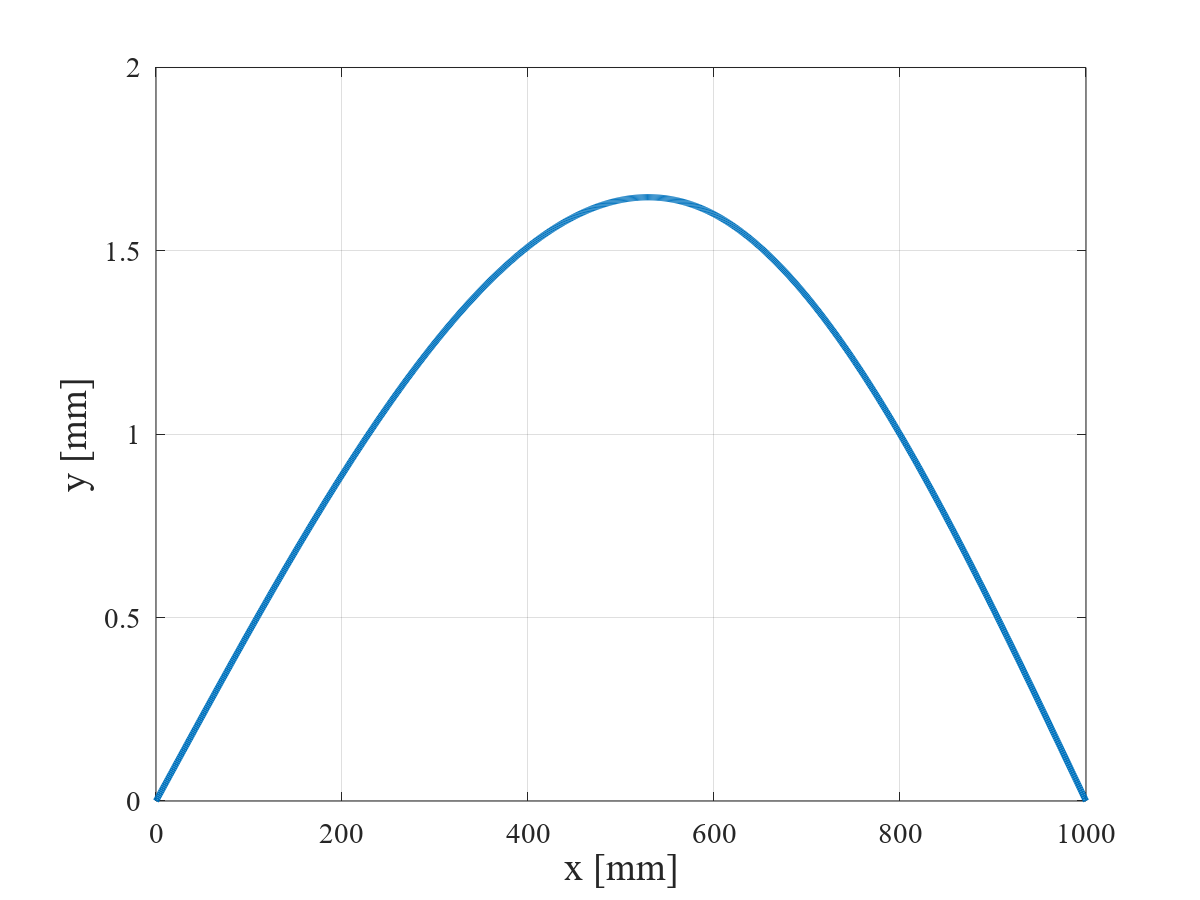
$P$ = 50 [N],$l$ = 1,000 [mm],$a$ = 600 [mm]($b$ = 400 [mm]),$E$ = 200,000 [N/mm2],$I_z$ = 3,000 [mm4]としたときの,たわみ曲線を図 5 に示す。集中荷重を受ける単純支持はりのたわみ曲線は三次関数で表される。
中央集中荷重のたわみ
単純支持はりの中央の集中荷重によるたわみを考える。たわみ曲線の式に,$a = l/2$,$b = l/2$ を代入する。
$0 ≤ x < a$ のたわみ
\[ y(x) = \frac{P}{48 E I_z}(-4x^3 + 3l^2 x) \]$a < x ≤ l$ のたわみ
\[ y(x) = \frac{P}{48EI_z}(-l^3 + 9l^2 x -12lx^2 +4x^3) \]はり中央のたわみ
$x = l/2$ を代入する。
\[ y(\frac{l}{2}) = \frac{P}{48 E I_z}\{-4(\frac{l}{2})^3 + 3l^2 \frac{l}{2}\} = \frac{Pl^3}{48 E I_z} \]演習問題
最大曲げ応力度
図のような荷重を受ける単純梁に断面 100 mm × 200 mm の部材を用いた場合,その部材に生じる最大曲げ応力度を求めよ。ただし,部材の自重は無視するものとする。(寸法の単位は mm とする。)

曲げ応力(bending stress)は中立面からの距離に比例して大きくなり,上下面でそれぞれ最大の圧縮および引張り応力を生ずる。中立面から上下面までの距離は $h/2$ であるから,最大曲げ応力度 $\sigma_\text{max}$ は,次式で求められる。ただし,$P$ は集中荷重 15 [kN],$M_\text{max}$ は最大曲げモーメント,$I_z$ は断面二次モーメントである。
\[ \sigma_\text{max}=\frac{M_\text{max}}{I_z}\times\frac{h}{2}=\frac{ab}{l}P\times\frac{12}{bh^3}\times\frac{h}{2}=0.03 \]よって,最大曲げ応力度は 30 [N/mm2](0.03 [kN/mm2])である。
曲げモーメント図
図-1のような荷重を受ける単純梁において,曲げモーメント図が図-2となる場合,荷重 $P$ の大きさを求めよ。


単純梁の左端を支点 A,右端を支点 B とし,それぞれの反力を $R_\text{A}$ [kN],$R_\text{B}$ [kN] とする。
\[ R_\text{A}+R_\text{B}=P+2P=3P \]支点を A 点としたとき,B 点でのモーメントのつり合いは次式で表される。
\[ P\times 3 + 2P \times 6 -R_\text{B}\times9=0 \]支点 B の反力 $R_\text{B}$ [kN] を求める。
\[ R_\text{B}=\frac{5}{3}P \]支点 A の反力 $R_\text{A}$ [kN] を求める。
\[ R_\text{A}=3P-R_\text{B}=\frac{4}{3}P \]支点 A から 3 m の位置で曲げモーメントが 8 [kN·m] となるので,次式が成り立つ。
\[ M=R_\text{A}x=\frac{4}{3}P \times 3 = 8 \]よって,荷重 $P$ の大きさは 2 [kN] となる。
(補足)SFD,BMD,たわみ曲線のグラフ化
本ページに掲載しているせん断力図(SFD),曲げモーメント図(BMD),たわみ曲線は,Octave により描画した。
Octave で,三角形状分布荷重を受ける単純支持はりのせん断力,曲げモーメント,たわみを計算し,SFD,BMD,たわみ曲線をグラフ化するプログラムは,以下のページで紹介している。