三角形状分布荷重を受ける単純支持はりのたわみ

2023年6月17日更新

はじめに

三角形状分布荷重を受ける単純支持はりのせん断力，曲げモーメントおよびたわみをわかりやすく，そして詳細に計算する。

検討モデル

三角形状に分布する荷重（以下，三角形状分布荷重。線形分布荷重ともいう。）を受ける単純支持はり（simply supported beam）のせん断力（shearing force），曲げモーメント（bending moment）およびたわみ（deflection）を検討するモデルを図 1 に示す。

単純支持はりの支点 A（単純支持はりの左端）は回転はできるが移動できない回転支点（hinged support），支点 B（単純支持はりの右端）は回転と共に一方に移動できる移動支点（movable support）とした。

単純支持はりの支点 A を $xy$ 座標の原点とし，原点より支点 B 方向を $x$ の正，原点より鉛直下向きを $y$ の正とする。また，はりの長さ（支点 A と支点 B との間の距離）は $l$ とする。

想定する荷重 $w(x)$ は，三角形状に分布する荷重とし，$w(0) = 0$，$w(l) = w_0$ とすれば，任意の $x$ の位置における荷重の大きさ $w(x)$ は，次式の一次関数で表わされる。

\[ w(x) = \frac{w_0}{l}x \]

用語の説明

曲げ荷重（bending load）: 支持されたはりを曲げるように作用する荷重
分布荷重（distributed load）: ある領域に分布して作用する力
たわみ（deflection）: 部材が外力などの作用によってわん曲したとき，荷重を受ける前の材軸線と直角方向の変位量

反力（reaction force）と全荷重のつり合い

単純支持はりの支点 A の反力 $R_A$ と支点 B の反力 $R_B$ の和は，三角形状に分布する全荷重 $\displaystyle \int^l_0 w(x) dx$ とつり合うので次式が成り立つ。

\[ R_A + R_B = \int^l_0 w(x) dx = \int^l_0 \frac{w_0}{l}x dx = [ \frac{w_0}{2l}x^2 ]^l_0= \frac{w_0 l}{2} \]

一方，支点を A 点としたときの B 点でのモーメントのつり合いは次式で表される。

\[ R_B l - \int^l_0 \frac{w_0}{l}x^2 dx = 0 \]

上式を $R_B$ で整理する。

\[ R_B = \frac{w_0 l}{3} \]

単純支持はりの支点 A の反力 $R_A$ は，反力と荷重のつり合いの式より，次のように求められる。

\[ R_A = \frac{w_0 l}{2} - R_B = \frac{w_0 l}{2} - \frac{w_0 l}{3} = \frac{w_0 l}{6} \]

単純支持はりの支点 B の反力 $R_B$ は，支点 A の反力 $R_A$ の 2 倍の大きさである。

せん断力（shearing force）

図 2 に示すように三角形状分布荷重を受ける単純支持はりを $x$ の位置で切断して考えると，その断面にはせん断力 $Q$ と曲げモーメント $M$ は，内力として作用する。

単純支持はりの支点 A から距離 $x$ におけるせん断力 $Q(x)$ は次式で表される。

\[ Q(x) = R_A - \int^x_0 w_0 \frac{\xi}{l} d\xi = \frac{w_0 l}{6} - \frac{w_0 x^2}{2l} \]

せん断力 $Q(x)$ を $x$ で微分すると，次式となる。

\[ \frac{\text{d}Q(x)}{\text{d}x} = -\frac{w_0}{2l}x \]

ここで，$x$ の取り得る範囲は，$0 \le x \le l$ であるから，$\text{d}Q/\text{d}x \le 0$ となり，せん断力 $Q(x)$ は，単純減少する。したがって，$x = 0$ でせん断力は最大，$x = l$ でせん断力は最小となり，最大値を $Q_{\text{max}}$，最小値を $Q_{\text{min}}$ とおくと，それぞれ次式で求めることができる。

\[ Q_{\text{max}} = Q(0) = \frac{w_0 l}{6} \] \[ Q_{\text{min}} = Q(l) = \frac{w_0 l}{6} - \frac{w_0 l}{2} = -\frac{w_0 l}{3} \]

また，せん断力の大きさが 0 となるときの $x$ は次式で求められる。

\[ Q(x) = \frac{w_0 l}{6} - \frac{w_0 x^2}{2l} = 0 \] \[ x = \frac{l}{\sqrt{3}} \]

せん断力図（SFD）

$w_0$ = 1 [N/mm]，$l$ = 1,000 [mm] としたときのせん断力図（SFD：Shearing Force Diagram）を図 3 に示す。三角形状分布荷重を受ける単純支持はりのせん断力は，単純減少する二次関数で表される。$x = l/\sqrt{3}$ = 577 [mm] において，せん断力は 0 [N] となる。また，せん断力の最大値と最小値は，次式で求められる。

\[ Q_{\text{max}} = Q(0) = \frac{w_0 l}{6} = 167 \text{ [N]} \] \[ Q_{\text{min}} = Q(l) = \frac{w_0 l}{6} - \frac{w_0 l}{2} = -\frac{w_0 l}{3} = -333 \text{ [N]} \]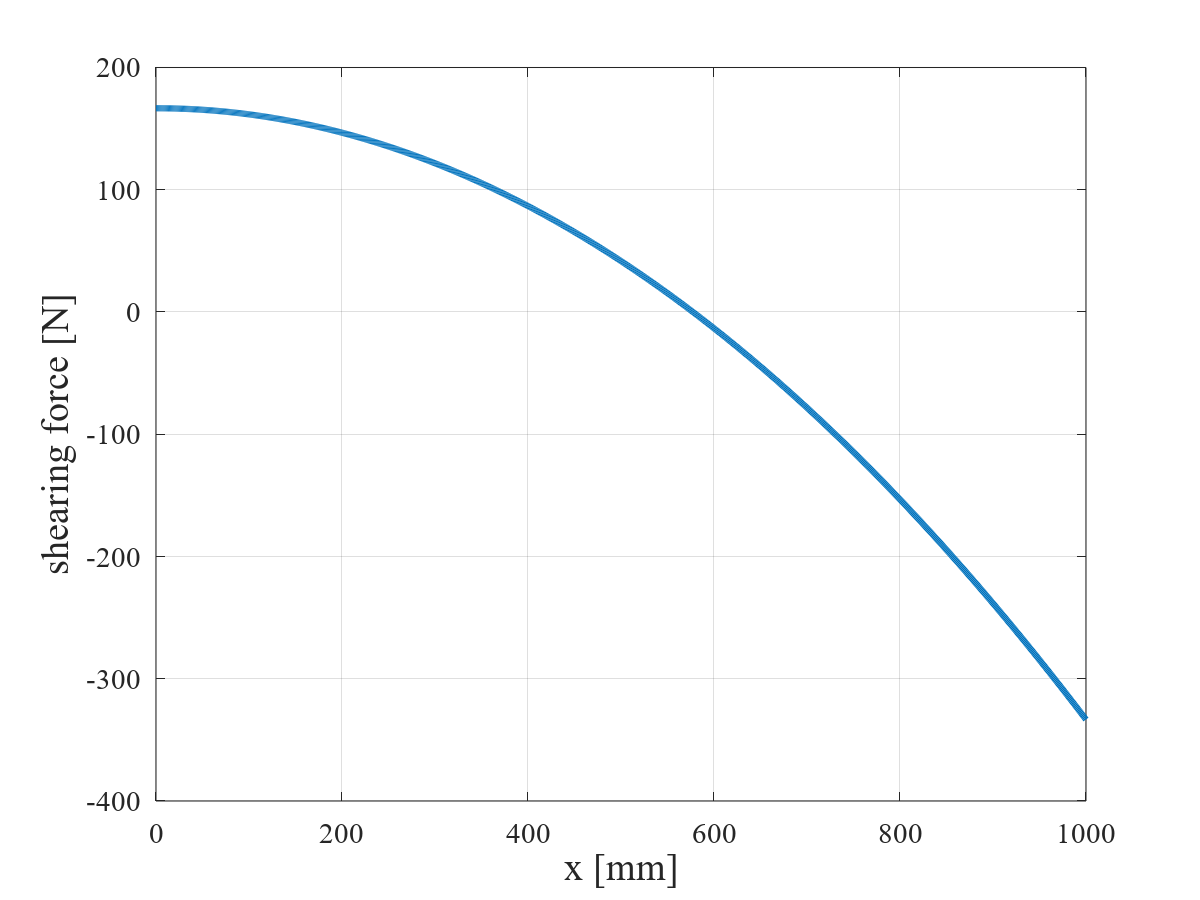

曲げモーメント（bending moment）

単純支持はりの支点 A から距離 $x$ における曲げモーメント $M(x)$ は，次式で表される。

\[ M(x) = R_A x - \int^x_0 w_0 \frac{\xi}{l}(x - \xi)d\xi = \frac{w_0 l}{6}x - \frac{w_0}{6l}x^3 \]

曲げモーメント $M(x)$ を $x$ で微分すると，次式となる。

\[ \frac{\text{d}M(x)}{\text{d}x} = \frac{w_0 l}{6} - \frac{w_0}{2l}x^2 \]

ここで，曲げモーメント $M(x)$ が最大となるときを求める。$M(0) = 0$，$\text{d}M(0)/\text{d}x \gt 0$，$M(l) = 0$，$\text{d}M(l)/\text{d}x \lt 0$ であり，曲げモーメントは上に凸の三次関数で表されることから，$\text{d}M(x)/\text{d}x = 0$ となる位置 $x_\text{M}$で，曲げモーメントは最大となる。よって，曲げモーメント $M$ が最大となる $x_\text{M}$ は次式で求められる。

\[ \frac{\text{d}M(x_\text{M})}{\text{d}x} = \frac{w_0 l}{6} - \frac{w_0 x_\text{M}^2}{2l} = 0 \] \[ x_\text{M} = \frac{l}{\sqrt{3}} \]

よって，曲げモーメントの最大値 $M_{\text{max}}$ は次式で求められる。

\[ M_{\text{max}} = M(x_\text{M}) = \frac{w_0 l}{6}x_\text{M} - \frac{w_0}{6l}x_\text{M}^3 = \frac{w_0 l}{6}\frac{l}{\sqrt{3}} - \frac{w_0}{6 l}\frac{l^3}{3\sqrt{3}} = \frac{\sqrt{3}}{27} w_0 l^2 \]

曲げモーメント図（BMD）

$w_0$ = 1 [N/mm]，$l$ = 1,000 [mm] としたときの，曲げモーメント図（BMD：Bending Moment Diagram）を図 4 に示す。三角形状分布荷重を受ける単純支持はりの曲げモーメントは，上に凸の三次関数で表される。$x_\text{M} = l/\sqrt{3} = 577$ [mm] において，曲げモーメントは最大となり，その大きさは 64,150 [N·mm] である。

\[ M_{\text{max}} = M(x_\text{M}) = \frac{\sqrt{3}}{27} w_0 l^2 = 64,150 \text{ [N·mm]} \]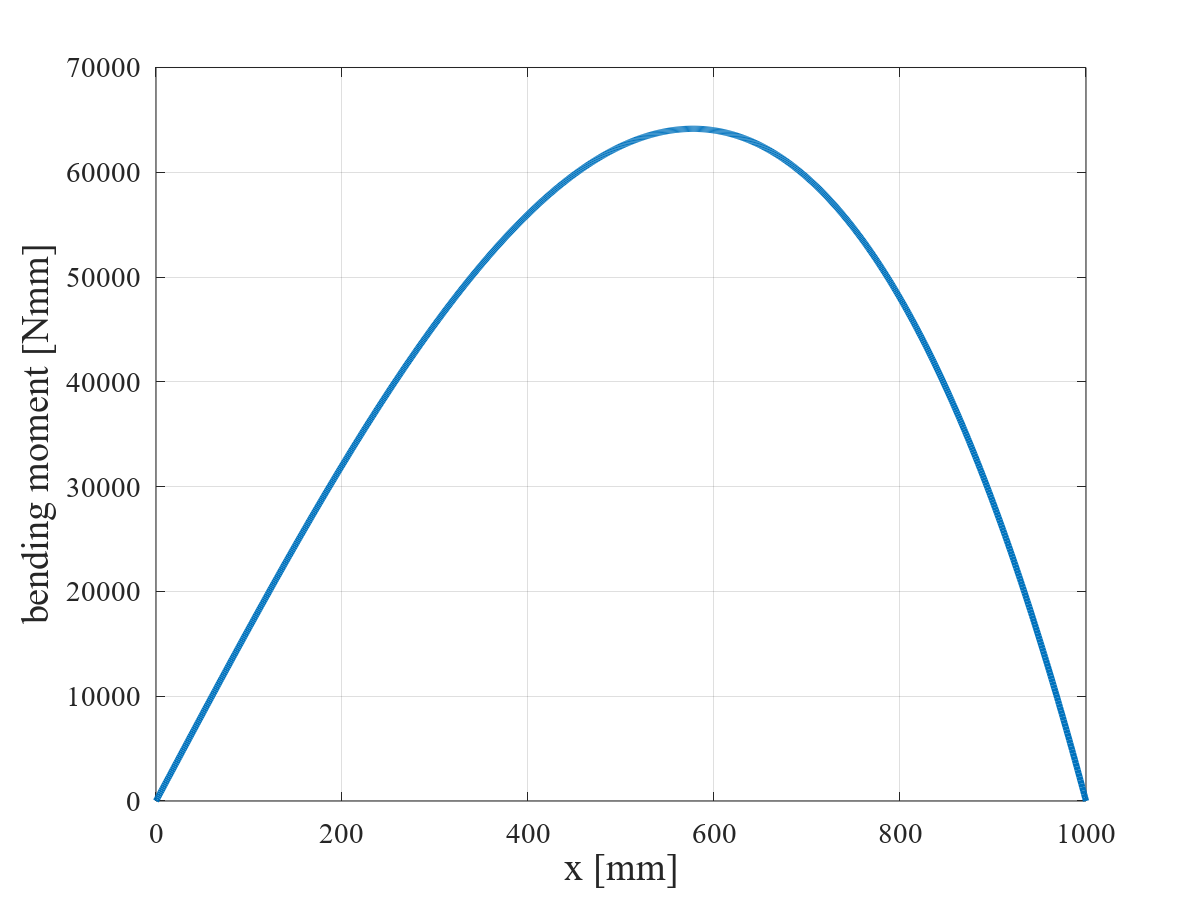

たわみ（deflection）

単純支持はりの支点 A から距離 $x$ におけるたわみ $y(x)$ に関する微分方程式は，次式で与えられる。この式は，弾性曲線方程式（elastic curve equation）である。

\[ \frac{\text{d}^2 y(x)}{\text{d}x^2} = -\frac{M}{EI_z} = \frac{w_0}{6EI_z l}(x^3-l^2 x) \]

ここで，$E$ は縦弾性係数（modulus of longitudinal elasticity）またはヤング率（Young's modulus），$I_z$ ははりの横断面の $z$ 軸に関する断面二次モーメント（moment of inertia of area）である。すなわち，この微分方程式は，「たわみの 2 階微分が曲げモーメントを剛性（$EI_z$）で割ったものを負にしたものに等しい」ことを意味する。

単純支持はりの場合，はりを固定する支点は変位しないと考えるため，弾性曲線はたわみ曲線（deflection curve equation）と一致する。

たわみ曲線の微分方程式を順次 $x$（断面の位置）で積分し，たわみ $y$ を求める。

\[ \frac{\text{d}y(x)}{\text{d}x} = \frac{w_0}{6EI_z l}(\frac{1}{4}x^4 - \frac{l^2}{2}x^2 + C_1) \] \[ y(x) = \frac{w_0}{6EI_z l}(\frac{1}{20}x^5 - \frac{l^2}{6}x^3 + C_1 x + C_2) \]

ここで，$C_1$，$C_2$ は積分定数であり，はりの境界条件（boundary condition）から決定される。まず，$x = 0$ において，$y = 0$ の境界条件より $C_2$ を求める。

\[ y(0) = \frac{w_0}{6EI_z l}C_2 = 0 \] \[ C_2 = 0 \]

さらに，$x = l$ において，$y = 0$ の境界条件より $C_1$ を求める。

\[ y(l) = \frac{w_0}{6EI_z l}(\frac{1}{20}l^5 - \frac{1}{6}l^5 + C_1 l) = 0 \] \[ C_1 = \frac{7}{60}l^4 \]

したがって，支点 A から距離 $x$ におけるたわみ $y(x)$は次式となる。

\[ y(x) = \frac{w_0}{360EI_z l}(3x^5 - 10 l^2x^3 + 7l^4x) \]

このようにしてはりのたわみを求める方法を重複積分法（double-integration method）という。

たわみ曲線（deflection curve）

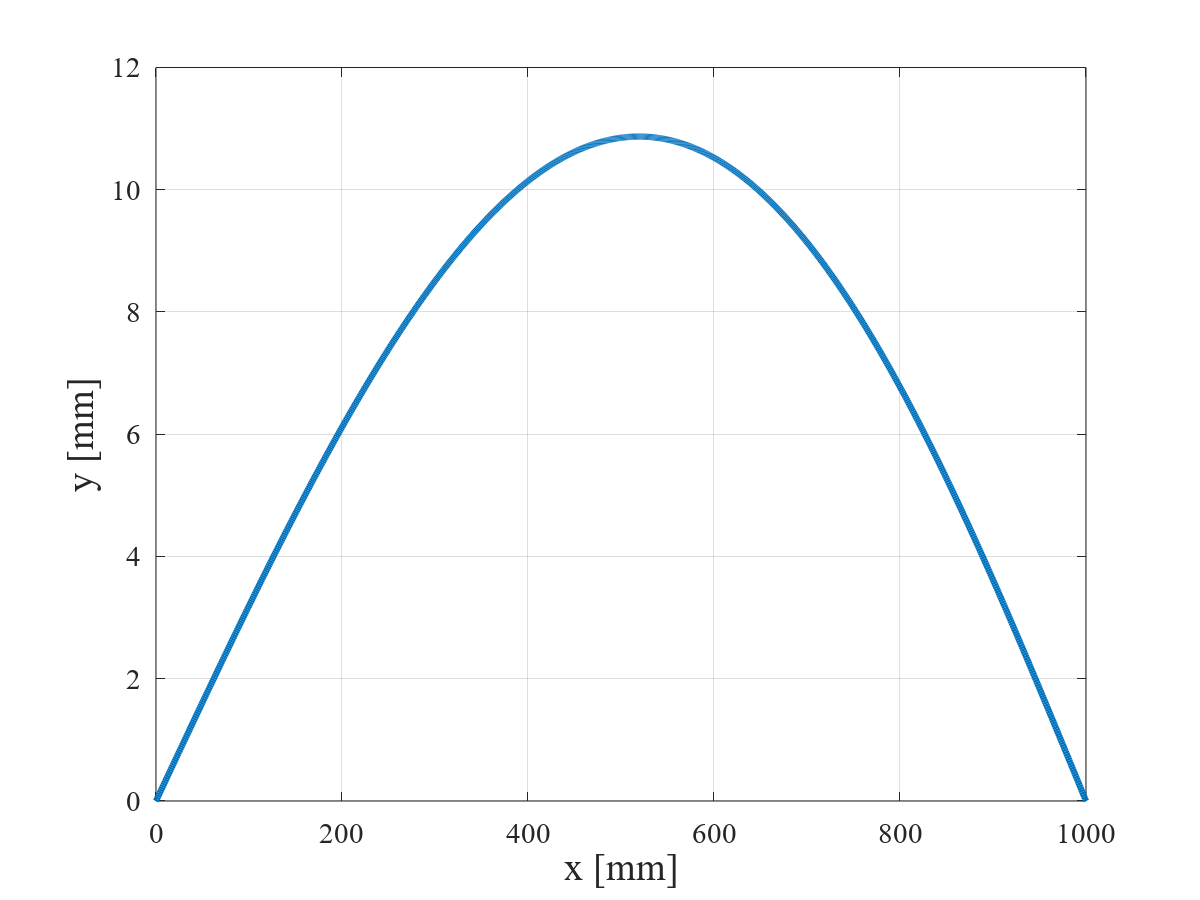
$w_0$ = 1 [N/mm]，$l$ = 1,000 [mm]，$E$ = 200,000 [N/mm²]，$I_z$ = 3,000 [mm⁴] としたときの，たわみ曲線を図 5 に示す。三角形状分布荷重を受ける単純支持はりのたわみ曲線は，上に凸の五次関数で表される。

与えられた条件では，$x$ が 518 [mm] において，たわみは最も大きくなり，その大きさは 10.87 [mm] である。

（補足）SFD，BMD，たわみ曲線のグラフ化

本ページに掲載しているせん断力図（SFD），曲げモーメント図（BMD），たわみ曲線は，Octave により描画した。

Octave で，三角形状分布荷重を受ける単純支持はりのせん断力，曲げモーメント，たわみを計算し，SFD，BMD，たわみ曲線をグラフ化するプログラムは，以下のページで紹介している。

三角形状分布荷重を受ける単純支持はりの SFD，BMD，たわみ曲線の計算・グラフ化【Masassiah Blog】