平成24年度 第1種 機械

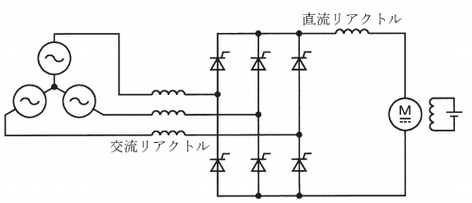
図のようにサイリスタ変換器の直流側に直流機の電機子巻線を接続した直流駆動システムを静止レオナードと呼ぶ。直流他励電動機を用いる場合，サイリスタ変換器の制御遅れ角 $\alpha$ を操作すると，直流機の回転速度を制御できる。電機子電流が連続であれば，軽負荷時の回転速度は，ほぼ $\cos\alpha$ に比例する。また，サイリスタがオンしているときの順方向電圧と交流及び直流リアクトルの抵抗が無視できる場合には，$\alpha$ を一定としたまま負荷トルクを増加すると，電機子巻線抵抗及び交流リアクトルの影響によって，負荷トルクにほぼ比例して回転速度は低下する。

図の回路構成の場合，$\alpha$ を操作するだけでは，制動トルクを発生することはできない。回生制動を行うためには，界磁電流の方向反転などが必要になる。界磁電流の方向反転を行って，直流機を回生制動する場合，サイリスタ変換器の $\alpha$ は 90 [°] 以上となる。

同期機に電機子電流が流れると，その起磁力によって界磁と同期して回転する基本波磁界が空隙中に生じ，これが界磁電流による磁界に影響を及ぼして電機子巻線での誘導起電力を無負荷状態から変化させる。これを電機子反作用といい，電機子反作用磁束に関するリアクタンスを電機子反作用リアクタンスという。任意の力率の電機子反作用磁束は直軸磁束及び横軸磁束に分けることができ，それぞれ対応するリアクタンスを直軸電機子反作用リアクタンス（$X_\text{ad}$）及び横軸電機子反作用リアクタンス（$X_\text{aq}$）という。

電機子電流による大部分の磁束は，電機子反作用磁束として電機子巻線及び界磁巻線と鎖交するが，一部の磁束は，電機子巻線だけと鎖交する。これが電機子漏れ磁束であり，電機子漏れリアクタンス（$X_\text{a}$）に対応する。

界磁電流による大部分の磁束は，電機子巻線及び界磁巻線と鎖交するが，一部の磁束は界磁巻線だけと鎖交する。これが界磁漏れ磁束であり，界磁漏れリアクタンス（$X_\text{F}$）に対応する。

円筒機のスロット内に収められた制動導体及び導電性くさび並びに突極機の磁極頭部の制動棒に漏れ磁束が存在する。これらの漏れ磁束に対応するのが直軸制動巻線漏れリアクタンス（$X_\text{Dd}$）及び横軸制動巻線漏れリアクタンス（$X_\text{Dq}$）である。

各巻線リアクタンスの回路に電機子巻線抵抗，界磁巻線抵抗，直軸及び横軸制動巻線抵抗を加えると，電機子端子側からの直軸及び横軸それぞれの等価回路ができる。この等価回路から，同期機の各リアクタンスを次のように求めることができる。

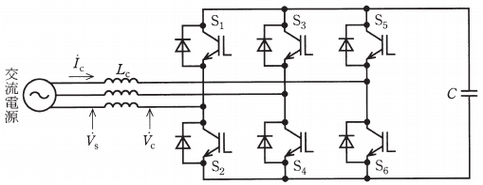
無効電力補償装置には交流系統に並列又は直列に接続する方式がある。並列接続方式の無効電力補償装置には，(a) サイリスタで位相制御したリアクトルと固定コンデンサとを並列接続した回路構成，(b) 連系リアクトルと電圧形自励変換器とを直列接続した回路構成，などがある。

図には，上述した (b) の電圧形自励変換器による無効電力補償装置の主回路構成を示す。この装置は，最近 STATCOM と呼ばれている。交流電源と自励変換器との間に連系リアクトルを挿入し，交流電源電圧 $\dot{V}_\text{S}$ に対して自励変換器が発生する交流電圧 $\dot{V}_\text{C}$ を調整する。このときの自励変換器の交流電流 $\dot{I}_\text{C}$ は，交流電源電圧の角周波数を $\omega_\text{S}$，連系リアクトルのインダクタンスを $L_\text{C}$ とすると次式となる。

\[ \dot{I}_\text{C}=\frac{\dot{V}_\text{S}-\dot{V}_\text{C}}{\text{j}\omega_\text{S}L_\text{C}} \]

したがって，$\dot{V}_\text{C}$ を調整することによって，交流電源から流れ込む遅れ進みの無効電流及び有効電流を制御することができる。$\dot{V}_\text{S}$ に対して $\dot{V}_\text{C}$ を同相にして，電圧の大きさ $|\dot{V}_\text{C}|$ を制御すると，無効電流だけを制御することができる。$|\dot{V}_\text{C}|$ を $|\dot{V}_\text{C}| \lt |\dot{V}_\text{S}|$ にしたときには，交流電源から遅れ電流が流れ込むことになる。

水素エネルギーはクリーンなエネルギーとして期待されている。この水素エネルギーを有効に利用できるものが燃料電池である。燃料電池では水素を燃料とし，酸化剤としては空気中の酸素とするものが最も多い。ここでは電気化学システムが用いられ，これは 2 本の電極と，その間に介在するイオン伝導帯である電解質とから成り立っている。2 本の電極のうち水素はアノードに供給され，ここでは酸化反応が起こる。

ここで得られる理論電圧はこの反応のギブズエネルギー変化によって決まる。水素と酸素から水ができる反応は発熱反応であり，高温では理論電圧は低くなる。また，得られる理論的な電気量はファラデーの法則から決まるが，具体的には消費する気体の体積に比例する。また，電気化学反応に関与する電子数も重要な要素であるが，水素 1 分子では 2 電子，酸素 1 分子では 4 電子が関与する反応となる。

変圧器の励磁電流は，鉄心の磁気飽和及びヒステリシスのため，巻線に正弦波を電圧を加えたとき，多くの奇数次高調波成分を含んだひずみ波となる。単相変圧器を単相回路で使用した場合は，このような励磁電流が流れて正弦波の誘導起電力が発生する。しかし，単相変圧器 3 台を中性点非接地の Y-Y 結線とした場合では必ずしも正弦波の誘導起電力が発生するわけではない。これを理論的に説明すると，次のようになる。

中性点が非接地の Y-Y 結線で，一次側の線間に正弦波電圧を加えた場合，二次側の線間電圧は正弦波電圧となる。しかし，中性点に向かう各相の励磁電流に含まれる 3 の倍数次の高調波は同相となるから，中性点が非接地のため零でなければならない。このため各相変圧器二次側の誘導起電力は高調波を含むひずみ波となる。

各相の変圧器二次側の誘導起電力を

\[ e_\text{u}=\sum_{n=1}^{\infty}\sqrt{2}E_n \sin(n\omega t +\phi_n) \] \[ e_\text{v}=\sum_{n=1}^{\infty}\sqrt{2}E_n \sin[n(\omega t - \frac{2\pi}{3})+\phi_n] \] \[ e_\text{w}=\sum_{n=1}^{\infty}\sqrt{2}E_n \sin[n(\omega t + \frac{2\pi}{3})+\phi_n] \]

とする。ただし，$n$ は奇数，$\omega$ は基本波の角周波数，$E_n$ 及び $\phi_n$ は $n$ 次高調波電圧の実効値及び位相である。u，v 間の線間電圧 $e_\text{uv}$ には高調波が存在しないから

\[ e_\text{uv}=e_\text{u}-e_\text{v}=\sqrt{6}E_1 \times \sin(\omega t + \phi_1 + \frac{\pi}{6}) \]

となる。②式が成立するには①式から

\[ \sum_{n=3}^{\infty}\sqrt{2}E_n{\sin(n\omega t + \phi_n)-\sin[n(\omega t - \frac{2\pi}{3})+\phi_n]}=0 \]

が成り立つ必要がある。③式について次の a.b.c. の高調波成分に分けて考える。

a. $n=$ $3\lambda$（$\lambda$ は正の奇数）の高調波の場合

\[ \sqrt{2}E_n [\sin(n\omega t + \phi_n) - \sin(n\omega t + \phi_n)] = 0 \]

となり，[ ] 内が零となるから，$E_n$ は零である必要はない。

b. $n=$ $3\lambda$ + 1（$\lambda$ は正の偶数）の高調波の場合

\[ \sqrt{2}E_n [\sin(n\omega t + \phi_n) - \sin(n\omega t - \frac{2\pi}{3} + \phi_n)] = 0 \]

となり，[ ] 内は零とならない。したがって，上式が零となるためには $E_n = 0$ が必要である。

c. $n=$ $3\lambda$ + 2（$\lambda$ は正の奇数）の高調波の場合

この場合も b. と同様に $E_n = 0$ となる必要がある。

このように，①式の誘導起電力には基本波のほかに a. の場合である多くの高調波，具体的には 3, 9, 15, ・・・次の高調波が含まれる可能性があり，実際にこのような高調波が観測されている。このため，中性点非接地の Y-Y 結線が使われるケースは少ない。

蛍光ランプ 40 形（消費電力 41 [W]，光束 3 450 [lm]，32 [本]）で，作業面で平均照度 750 [lx] を維持している事務室（8.0 [m] × 10.0 [m]，天井高さ 2.7 [m]）がある。この照明設備を LED ランプ（消費電力 28 [W]，光束 2 300 [lm]）に改修したい。

光束法の計算式を基に，蛍光ランプを用いた場合の照明率を手掛かりとして，LED ランプを用いた場合の平均照度等を以下の手順で求めて比較する。ただし，作業面は事務室の床面と同じ面積とする。保守率は，蛍光ランプ及び LED ランプとも 0.75 とする。また，LED ランプを用いた場合の照明率は，照明器具内での光損失が減少するため，蛍光ランプを用いる場合より 8 [%] 改善され 1.08 倍になるものとする。

1. 平均照度 750 [lx] を維持するのに必要な作業面への入射光束は 60 000 [lm] である。
2. 蛍光ランプを用いた場合の照明率は，作業面への入射光束と蛍光ランプの総光束との関係から 0.72 が求まる。
3. この照明率を手掛かりに，蛍光ランプと同数量の LED ランプを用いた場合の平均照度を計算すると 540 [lx] になる。
4. また，この作業面に LED ランプで照明し，蛍光ランプと同等の平均照度 750 [lx] を維持するには，LED ランプが 45 [本] 必要になる。
5. この作業面で平均照度 750 [lx] を維持するのに必要な総消費電力は，蛍光ランプに対し，LED ランプでは約 96 [%] になる。

メカトロニクス分野で多用されている圧力センサとして，ストレインゲージが挙げられる。これは，素子のひずみで抵抗値が変化することを利用したセンサである。

ストレインゲージは，次のような特徴をもつ 2 種類の素子で分類される。特に抵抗変化率 $\displaystyle \frac{\Delta R}{R}$ のひずみ $\epsilon$ に対する比 $\displaystyle K(=\frac{\Delta R/R}{\epsilon})$ はゲージ率と呼ばれ，この値はストレインゲージの素子によって大きく異なる。

金属ストレインゲージ

ひずみが発生すると，金属の長さが変化し，素子の電気抵抗が変化する性質を利用したものである。上記の $K$ が 2 程度であり，抵抗の変化量が小さい。

半導体ストレインゲージ

ひずみが発生すると，キャリア密度や移動度が変化するピエゾ抵抗効果によって素子特性そのものの抵抗率が変化する性質を利用しており，$K$ も 100 ～ 300 と大きく，広く普及してきている。また，この電気抵抗の温度特性は金属と異なり，温度が高くなると電気抵抗が低くなる性質がある。

これらのひずみゲージの微小な抵抗変化を測定するため，一般的には，測定抵抗を含んで四つの抵抗をブリッジ状に配置して，中間点の電位差を測定するホイートストンブリッジ回路が利用される。