平成30年度 第二種 電気主任技術者二次試験 機械・制御
目次
問1 三相かご形誘導電動機の始動方式
三相かご形誘導電動機の始動方式に関し,次の問に答えよ。
- 数キロワット以上の中小容量の三相かご形誘導電動機を全電圧始動した場合,定格電流の 5 ~ 8 倍程度の始動電流が流れる。この始動電流によって電動機に関連する設備に生じる可能性がある問題点を二つ挙げよ。
- スターデルタ始動方式を用いた場合,始動電流をほぼ $\displaystyle \frac{1}{3}$ にすることができる。その理由を述べよ。
- スターデルタ始動方式を用いて始動電流を低減させた場合の問題点を二つ挙げよ。
- インバータを用いて,周波数及び電圧を制御して始動し,定格速度まで連続的に加速するインバータ始動方式の優位な点を二つ挙げよ。
1. 始動電流によって電動機に関連する設備に生じる可能性がある問題点
三相かご形誘導電動機を全電圧始動した場合,次のような問題が生じる可能性がある。
- 過大な始動電流のため,大きな電圧降下を生じる。
- 過大な始動電流のため,遮断器(ブレーカ)が動作する。
- 過大な始動電流のため,配線が焼損する可能性がある。
- 始動電流に対応するため,定格設備容量より過大な設備容量が必要となる。
- 始動時の機械的ショックが大きい。
- 始動電流値に対応する保護機器を選定すると,平常時に適切な保護機能が得られない。
2. 始動電流を 1/3 にすることができる理由
スターデルタ始動方式は電動機の各相の巻線を,始動時にはスター結線とすることによって相電圧が $1/\sqrt{3}$ となり,始動終了後デルタ結線に切り換えることによって電源電圧を各相に供給する方式である。スター結線時はデルタ結線時と比較して電源から見た見かけ上のインピーダンスが 3 倍となるので,線電流が 1/3 となる。
3. スターデルタ始動方式を用いた場合の問題点
スターデルタ始動方式を用いて始動電流を低減させた場合の問題点として,次のようなものがある。
- 始動トルクが約 1/3 に低下するため,適用できる負荷が限られる。
- 始動トルクが低下するので,始動時間が長くなる。
- スター結線からデルタ結線に切り換える際に過大な突入電流が生じることがある。
- 切換え時の電源位相によっては過大な突入電流が生じ,遮断器(ブレーカ)が動作する。
- 切換え時の無電圧時間は電動機が空転するため,デルタ投入時に機械的ショックを生じる。
4. インバータ始動方式の優位な点
インバータを用いて,周波数及び電圧を制御して始動し,定格速度まで連続的に加速するインバータ始動方式には,次のような優位な点がある。
- 通常は $V/f$ を基本とし,電圧特性に補正を施した制御を行うので,低周波低電圧でも磁束が低下せず始動トルクが低下しない。
- 始動電流が定格電流の 2 倍程度以下になる
- 始動時間をインバータによって制御できる。
- 始動帰還に生じる電動機の損失が少なく,発熱を抑制できる。
- ソフトスタートにより始動による機械的ショックが小さい。
- 始動電流や突入電流による他の機器への影響が少ない。
問2 三相星形接続の円筒形同期発電機
図は,三相星形接続の円筒形同期発電機のフェーザ図である。この図を参照して次の問に答えよ。ただし,電機子抵抗による電圧降下及び磁気飽和は無視するものとする。
- $E$ [V],$V$ [V],$\delta$ [rad],$X_\text{S}$ [Ω] を用いて,発電機出力 $P$ [kW] を表す式を導出過程を含めて示せ。
- 定格皮相電力 30 000 kV·A,定格端子電圧(線間電圧)6 600 V,短絡比 0.5 の円筒形三相同期発電機において,次の a,b 及び c の問に答えよ。
- $X_\text{S}$ [Ω] の値を求めよ。
- 三相平衡交流系統に接続して,$E=7000$ V,$V=3810$ V,$\delta = \pi/6$ rad で運転しているときの $P$ [kW],$I$ [A],力率($\cos\phi$)の値を求めよ。
- この発電機を三相平衡交流系統から切り離して,三相平衡抵抗器負荷に接続した。界磁電流を調整して $V=3700$ V,$\delta = \pi/3$ rad で運転し,抵抗器負荷に電力を供給した。このときの $P$ [kW],$E$ [V],$I$ [A],力率($\cos\phi$)の値を求めよ。

1. 発電機出力 $P$
発電機出力 $P$ は次式で表される。
\[ P=3VI\cos\phi \times 10^{-3} \]一方,フェーザ図より次式が成り立つ。
\[ X_\text{S}I\cos\phi=E\sin\delta \]上の 2 式より,発電機出力 $P$ を表す式を求める。
\[ P=3V\frac{E\sin\delta}{X_\text{S}}\times10^{-3}=\frac{3EV}{X_\text{S}}\sin\delta\times10^{-3} \text{ [kW]} \]2. a. 同期リアクタンス $X_\text{S}$ [Ω] の値
定格電機子電流 $I_\text{R}$ は次式で求められる。
\[ I_\text{R}=\frac{30000\times10^3}{\sqrt{3}\times6600}=2624.3 \text{ [A]} \]1 p.u. インピーダンスは,定格端子電圧(相電圧)を定格電機子電流で除して求める。
\[ Z_\text{p.u.}=\frac{6600/\sqrt{3}}{2624.3}=1.452 0 \]単位法において,同期リアクタンスは短絡比の逆数(= 1/0.5)であり,同期リアクタンス $X_\text{S}$ [Ω] は次式で求められる。
\[ X_\text{S}=\frac{1}{0.5}\times1.452 0=2.9040 \]同期リアクタンス $X_\text{S}$ [Ω] の値は 2.90 Ω である。
2. b. 三相平衡交流系統に接続時の $P$ [kW],$I$ [A],力率($\cos\phi$)の値
発電機出力 $P$ [kW] は次式で求められる。
\[ P=\frac{3EV}{X_\text{S}}\sin\delta\times10^{-3}=\frac{3\times7000\times3810}{2.9040}\times\sin{\frac{\pi}{6}}\times10^{-3}=13776 \text{ [kW]} \]フェーザ図より,$IX_\text{S}$ は次式で求められる。
\[ IX_\text{S} =\sqrt{E^2-2EV\cos\delta+V^2} \] \[ IX_\text{S} =\sqrt{7000^2-2\times7000\times3810\cos{\frac{pi}{6}}+3810^2} \] \[ IX_\text{S} =\sqrt{1.7322\times10^7}=4162.0 \]よって,電機子電流 $I$ は次式となる。
\[ I=\frac{4162.0}{X_\text{S}}=\frac{4162.0}{2.9040}=1433.2 \]力率($\cos\phi$)は次式で求められる。
\[ \cos\phi=\frac{P\times10^3}{3VI}=\frac{13776\times10^3}{3\times3810\times1433.2}=0.840 95 \]以上より,$P$ は 13 800 [kW],$I$ [A] は 1 430 [A],力率($\cos\phi$)は 0.841 である。
2. c. 三相平衡抵抗器負荷に接続時の $P$ [kW],$E$ [V],$I$ [A],力率($\cos\phi$)の値
抵抗負荷のため,$\cos\phi=1.00$,$\phi=0$ rad である。
フェーザ図より次式が成り立つ。
\[ E\cos\delta=V+I_\text{S}\sin\phi=V \] \[ E=\frac{V}{\cos\delta}=\frac{3700}{0.5}=7400.0 \]同じくフェーザ図より次式が成り立つ。
\[ P=3V\frac{E\sin\delta}{X_\text{S}}\times10^{-3}=\frac{3\times7400\times3700}{2.904 0}\sin{\frac{\pi}{3}}\times10^{-3}=24496 \]電機子電流 $I$ を求める。
\[ I=\frac{P\times10^3}{3V\cos\phi}=\frac{24496\times10^3}{3\times3700\times1.00}=2206.8 \]以上より,三相平衡抵抗器負荷に接続時の $P$ は 24 500 [kW],$E$ は 7 400 [V],$I$ は 2 210 [A],力率($\cos\phi$)は 0 rad である。
問3 三相サイリスタ変換器を 2 台使用した変換装置
準備中


問4 2 自由度制御系
図 1 のような 2 自由制御系がある。ここで $G(s)$ は制御対象,$C(s)$ 及び $F(s)$ は補償器である。また,$R(s)$ は目標値,$D(s)$ は外乱,$Y(s)$ は制御量,$E(s)$ は制御偏差である。この制御系について,次の問に答えよ。
- 図 1 に示すフィードバック補償器 $C(s)$ の係数 $K_\text{P}$ 及び $T_\text{I}$ の名称を答えよ。
- $K_\text{P}=10$,$T_\text{I}=0.1$ のとき,$C(s)$ の角周波数 $\omega$ [rad/s] に対するゲイン特性の概形を答案用紙に印刷されている図 2 に折れ線近似で図示せよ。
- $R(s)=0$ として,外乱 $D(s)$ から制御偏差 $E(s)$ までの閉ループ伝達関数を求めよ。
- 上記小問 3. で求めた閉ループ伝達関数において,固有角周波数が 5 rad/s,減衰係数が 0.7 となるように,$K_\text{P}$ と $K_\text{I}$ の値を定めよ。
- $D(s)=0$ として,目標値 $R(s)$ から制御量 $Y(s)$ までの閉ループ伝達関数を $F(s)$,$C(s)$,$G(s)$ を用いて求めよ。
- 上記小問 3. で求めた閉ループ電圧関数は $F(s)$ に依存しない。また,上記小問 5. で求めた閉ループ伝達関数 $C(s)$ に依存しない。これは制御系にどんな特長をもたらすか答えよ。この性質を利用しているのが 2 自由度制御系である。


1. フィードバック補償器 $C(s)$ の係数 $K_\text{P}$ 及び $T_\text{I}$ の名称
フィードバック補償器 $C(s)$ の係数 $K_\text{P}$ 比例ゲイン,$T_\text{I}$ は積分時間である。
2. ゲイン特性の概形
フィードバック補償器 $C(s)$ の伝達関数を変形する。
\[ C(s)=K_\text{P}(1+\frac{1}{T_\text{I}s})=K_\text{P}\times\frac{1}{T_\text{I}s}\times(1+T_\text{I}s) \]フィードバック補償器 $C(s)$ の周波数伝達関数は,次式となる。
\[ C(\text{j}\omega)=K_\text{P}\times\frac{1}{\text{j}T_\text{I}\omega}\times(1+\text{j}T_\text{I}\omega) \]周波数伝達関数のゲイン特性は,次式となる。
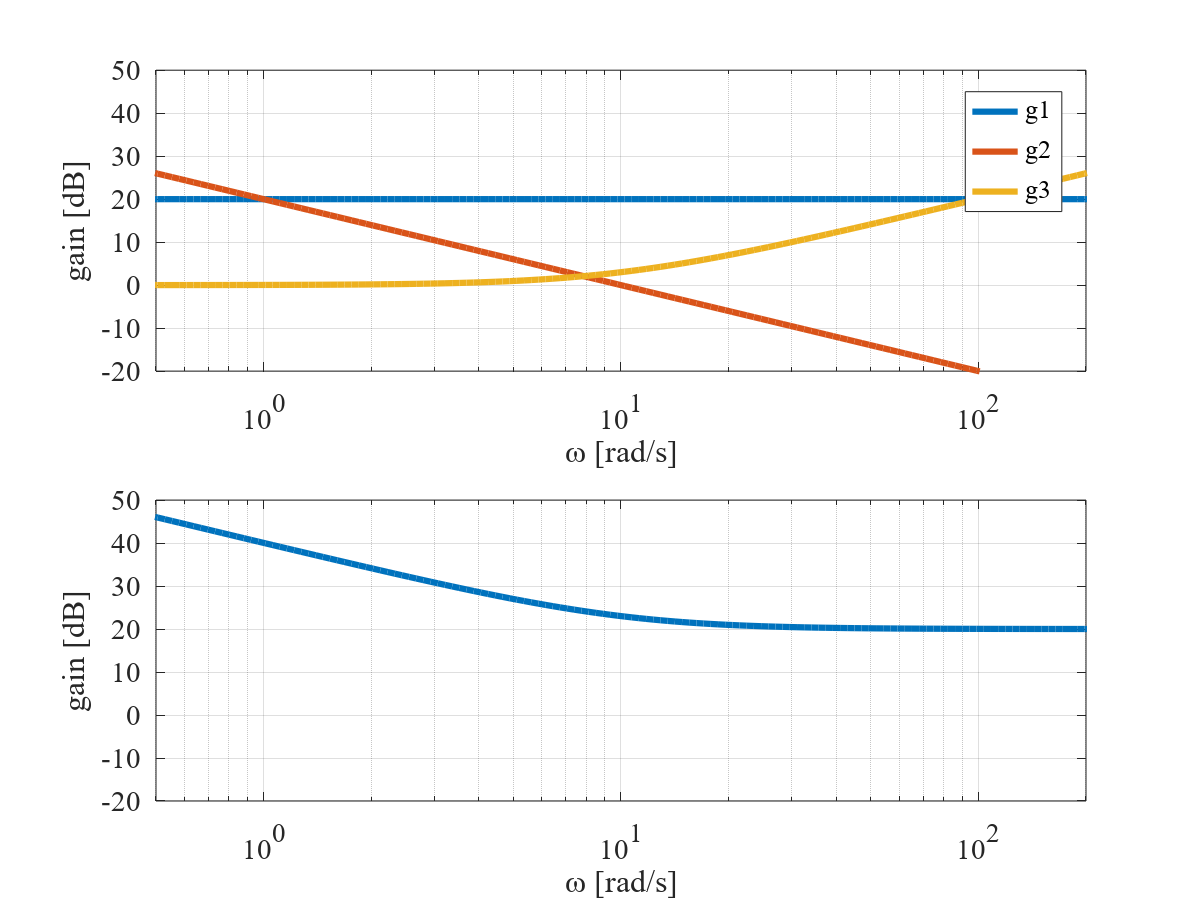
\[ 20\log_{10}{|C(\text{j}\omega)|}=20\log_{10}{K_\text{P}}+20\log_{10}{|\frac{1}{\text{j}T_\text{I}\omega}|}+20\log_{10}{|1+\text{j}T_\text{I}\omega|} \]ゲイン特性の概形は次の図のようになる。上式の第一項のゲイン特性 g1 は 20 dB で一定,第二項のゲイン特性 g2 は勾配 -20 dB/dec の直線であり,ゲインが 0 dB となるときの角周波数は 10 rad/s,第三項のゲイン特性 g3 は,$\omega$ < 10 の領域では 0 dB,$\omega$ > 10 の領域では 20 dB/dec の勾配の直線に近似できる。以上の 3 つのゲイン特性を加え合わせたものが,補償器 $C(s)$ のゲイン特性である。
3. 外乱 $D(s)$ から制御偏差 $E(s)$ までの閉ループ伝達関数
図 1 において,外乱 $D(s)$ から制御偏差 $E(s)$ までの閉ループ伝達関数は,次のように計算される。
\[ \frac{E(s)}{D(s)}=\frac{-G(s)}{1+C(s)G(s)}=\frac{-\frac{1}{4s+1}}{1+\frac{K_\text{P}(T_\text{I}s+1)}{T_\text{I}s(4s+1)}}=\frac{-T_\text{I}s}{4T_\text{I}s^2+T_\text{I}(K_\text{P}+1)s+K_\text{P}} \]4. $K_\text{P}$ と $K_\text{I}$ の値
小問 3. で求めた閉ループ伝達関数の分母多項式は,次式となる。
\[ s^2+\frac{K_\text{P}+1}{4}s+\frac{K_\text{P}}{4T_\text{I}} \]一方,固有角周波数 $\omega_\text{n} = 5$ rad/s,減衰係数 $\xi=0.7$ となる 2 次系の分母多項式は,次式となる。
\[ s^2+2\xi\omega_\text{n}s+\omega_\text{n}^2=s^2+7s+25 \]上の 2 式の係数を比較する。
\[ \frac{K_\text{P}+1}{4}=7 \] \[ \frac{K_\text{P}}{4T_\text{I}}=25 \]よって,$K_\text{P}=27$,$T_\text{I}=0.27$ である。
5. 目標値 $R(s)$ から制御量 $Y(s)$ までの閉ループ伝達関数
図 1 のブロック線図より次の関係式が成り立つ。
\[ ((F(s)R(s)-Y(s))C(s)+\frac{F(s)}{G(s)}R(s))G(s)=Y(s) \]これを変形する。
\[ \frac{Y(s)}{R(s)}=F(s) \]すなわち,$G(s)$ 及び $C(s)$ の形によらず,$R(s)$ から $Y(s)$ までの目標値応答特性は $F(s)$ となる。
6. 制御系にもたらす特長
目標値応答特性は $F(s)$ で指定することができる。一方,外乱に対するフィードバック制御特性は $C(s)$ で指定できる。このように,二つの補償器 $F(s)$ と $C(s)$ を用いて,目標値応答特性とフィードバック制御特性を独立に指定できる特長がある。