令和3年度 第2種 機械・制御
目次
受験者は 2,407 人,合格者数は 413 人で,合格率は 17.2 % だった。
合格基準は,100 点満点換算で 56.7 点以上(実得点 180 点満点で 102 点以上),かつ,各科目ともに平均点 -5 点以上である。
問1 滑り s で運転している三相誘導電動機
滑り $s$ で運転している三相誘導電動機の星形結線一相当たりの L 形等価回路を下図に示す。回路定数はそれぞれ以下のとおりである。ただし,等価回路の端子電圧(相電圧)を $V_1$,入力電流を $I_1$,電源周波数を $f$,極対数を $p$ とし,等価回路の励磁コンダクタンス $g_0$ 及び励磁サセプタンス $b_0$ は無視できるものとする。
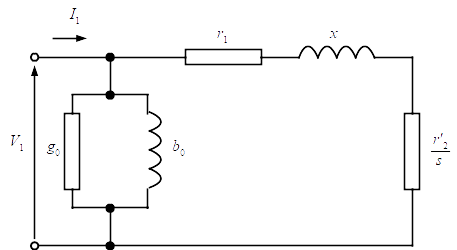
- $g_0$ : 励磁コンダクタンス
- $b_0$ : 励磁サセプタンス
- $r_1$ : 一次抵抗
- $r'_2$ : 一次換算二次抵抗
- $x$ : 漏れリアクタンス
次の問については,図に記載されている記号を用いて答えよ。
(1) 入力電流 $I_1$ の式を求めよ。
(2) 機械的出力 $P_o$ の式を求めよ。
(3) 同期角速度 $\omega_\text{s}$ を電源周波数 $f$ 及び極対数 $p$ を用いて表せ。
(4) この誘導電動機の発生トルク $T$ の式を求めよ。
(5) 最大トルクが得られる滑り $s_\text{m}$ の式を求めよ。
(6) 最大トルク $T_\text{m}$ の式を求めよ。
問1 解答と解説
準備中
(1) 入力電流 $I_1$
(2) 機械的出力 $P_o$
(3) 同期角速度 $\omega_\text{s}$
(4) 誘導電動機の発生トルク $T$
(5) 滑り $s_\text{m}$
(6) 最大トルク $T_\text{m}$
問2 単相変圧器の短絡試験
容量 200 kV·A,一次電圧 11 000 V,二次電圧 440 V,周波数 50 Hz を定格とし,自己容量基準の短絡インピーダンス $\%z$ が 4.5 % の単相変圧器がある。この変圧器の二次側を短絡し一次側に定格電流を流したときの一次側の電力計の指示値は 1.5 kW であった。
この変圧器について,次の問に答えよ。ただし,変圧器の励磁電流,鉄損は無視できるものとする。
(1) $\%z$ のうち抵抗分($\%r$),リアクタンス分($\%x$)を答えよ。
(2) 短絡インピーダンスの一次換算値 $Z$ [Ω] を答えよ。
(3) $Z$ [Ω] の抵抗分 $R$ [Ω] 及び,リアクタンス分 $X$ [Ω] を答えよ。
(4) この変圧器の二次側にリアクトルを接続し,一次側に交流 11 000 V を加えたときの二次電流は 400 A であった。このときの変圧器二次電圧 $V_2$ [V] 及び,リアクトルの無効電力 $Q_\text{L}$ [kvar] を求めよ。なお,リアクトルの抵抗分は無視してよい。
問2 解答と解説
(1) $\%z$ のうち抵抗分($\%r$),リアクタンス分($\%x$)
短絡インピーダンスの抵抗分を $R$ [Ω] とすると,$\%r$ [%] は次式で定義される。ここに $P_\text{loss}$ は二次短絡試験の電力 1.5 [kW],$P_0$ は変圧器定格容量 200 [kV·A],$V_1$ は変圧器一次電圧 11 000 [V],$I_1$ は変圧器一次定格電流 [A] である。
\[ \%r=\frac{R\times I_1}{V_1}\times 100 = \frac{R \times {I_1}^2}{V_1 \times I_1} \times 100 = \frac{P_\text{loss}}{P_0}\times 100 = \frac{1.5}{200} \times 100 = 0.75 \]$\%z$ のうちリアクタンス分 $\%x$ は次式で求められる。
\[ \%x=\sqrt{\%z^2 - \%r^2} = \sqrt{4.5^2 - 0.75^2}=\sqrt{20.25 - 0.562 5} \approx 4.4371 \]したがって,$\%r=0.75$ %,$\%x=4.44$ % である。
(2) 短絡インピーダンスの一次換算値 $Z$ [Ω]
$\%z$ と実インピーダンス $Z$ [Ω] の関係は定格電圧と定格容量により,次式で示される。
\[ Z=\%z \times \frac{1}{100} \times \frac{{V_1}^2}{P_0} \]ここでは一次換算を求めるので,$V_1$ を一次電圧,$P_0$ を変圧器容量として以下となる。
\[ Z=4.5 \times \frac{1}{100} \times \frac{11000^2}{200000}=27.225 \]よって,$Z=27.2$ Ω である。
(3) $Z$ [Ω] の抵抗分 $R$ [Ω] 及び,リアクタンス分 $X$ [Ω]
小問 (1) で求めた抵抗分とリアクタンス分のパーセント値及び小問 (2) の $Z=27.225$ Ω を使って,次式のように求められる。
\[ R=\frac{\%r}{\%z}\times Z = \frac{0.75}{4.5} \times 27.225 = 4.537 5 \] \[ X=\frac{\%x}{\%z}\times Z = \frac{4.437}{4.5} \times 27.225 = 26.884 \]よって,$R=4.54$ Ω,$X=26.9$ Ω である。
(4) 変圧器二次電圧 $V_2$ [V] 及び,リアクトルの無効電力 $Q_\text{L}$ [kvar]
変圧器の一次,二次の巻数比は $a=25$(11 000 : 440)であるので,一次電流 $I_1$ は,次式で求められる。
\[ I_1 = \frac{1}{a}\times I_2 = \frac{1}{25} \times 400 = 16 \text{ [A]} \]皮相電力 $S$ は,次式で求められる。
\[ S = 11000 \times 16 = 176 000 \text{ [V·A]} \]負荷リアクトルの抵抗は 0 Ω であるので,回路の有効電力は変圧器巻線の抵抗による分の次式で表される。(回路の有効電力は,すなわち変圧器巻線の有効電力 $P_\text{c}$)
\[ P_\text{c}=R\times 16^2 = 4.5375 \times 16^2 = 1161.6 \text{ [W]} \]変圧器巻線による無効電力 $Q_\text{c}$ は,次式で求められる。
\[ Q_\text{c}=X\times 16^2 = 26.844 \times 16^2 = 6872.1 \text{ [var]} \]二次側負荷リアクトルの無効電力を $Q_\text{L}$ [var] とすると次式が成立し,これを解いて,$Q_\text{L}$ を求める。
\[ S=\sqrt{{P_c}^2+(Q_\text{c}+Q_\text{L})^2} \] \[ Q_\text{L}=\sqrt{S^2 - {P_c}^2} - Q_\text{c} = \sqrt{(176000)^2 - (1161.6)^2} - 6872.1 = 169 120 \text{ [var]} \approx 169 \text{ [kvar]} \]二次電圧 $V_2$ は,次式で求められる。
\[ V_2 = \frac{169120}{400}=422.8 \approx 423 \text{ [V]} \]よって,変圧器二次電圧 $V_2 = 423$ [V],リアクトルの無効電力 $Q_\text{L} = 169$ [kvar] である。
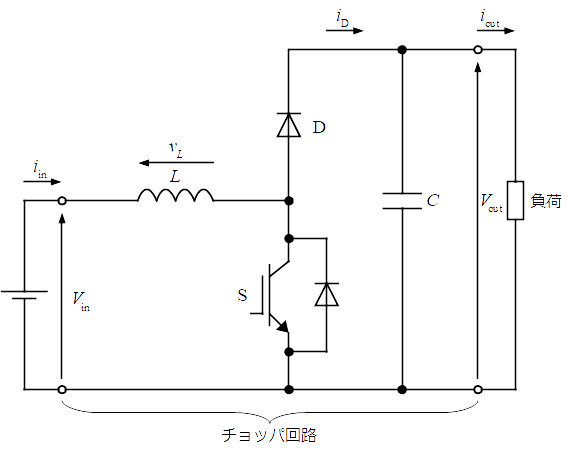
問3 IGBT をスイッチングデバイスに用いたチョッパ回路
図は IGBT をスイッチングデバイス S(以下,デバイス S と略す)に用いたチョッパ回路である。このチョッパの機能は,キャパシタンス $C$ とコンデンサとリアクタンス $L$ のリアクトルの働きによって実現されている。入力は直流電圧 $V_\text{in}$(一定値),出力は $V_\text{out}$ である。デバイス S は,$T_\text{on}$ の時間はオン,$T_\text{off}$ の時間はオフを繰り返し,周期は一定で,$T_\text{on} + T_\text{off}$ である。入力電流 $i_\text{in} \gt 0$,全ての回路素子は理想的と仮定して,次の問に答えよ。
(1) このチョッパ回路は太陽光発電でよく用いられている。その理由についてチョッパ回路の $V_\text{in}$ と $V_\text{out}$ の大小関係に触れつつ簡単に述べよ。
(2) $T_\text{on}$ の時間において,リアクトルの電圧 $v_\text{L}$ を求めよ。また,求めた式をもとに電流 $i_\text{in}$ は増加するか,減少するか述べよ。
(3) $T_\text{off}$ の時間において,リアクトルの電圧 $v_\text{L}$ を求めよ。また,求めた式をもとに電流 $i_\text{in}$ は増加するか,減少するか述べよ。
次に,コンデンサのキャパシタンス $C$ は十分に大きく,チョッパの出力電圧は一定値 $V_\text{out}$ に平滑されているものとする。さらに,電流 $i_\text{in}$ のリプルが十分に小さく一定値 $I_\text{in}$ と見なせると仮定する。このとき,
(4) ダイオード D に流れる電流 $i_\text{D}$ の平均値 $I_\text{D}$ を $T_\text{on}$,$T_\text{off}$,$I_\text{in}$ を用いて示せ。
(5) 出力電圧 $V_\text{out}$ を $T_\text{on}$,$T_\text{off}$,$V_\text{in}$ を用いて示せ。
問3 解答と解説
(1) このチョッパ回路が太陽光発電で良く用いられている理由
解答例1
太陽光発電で発電した直流電圧をより高い電圧のバッテリに充電するから,入力 $V_\text{in}$ よりも出力 $V_\text{out}$ が大きい。
解答例2
系統の電圧波高値が太陽光発電の電圧よりも高いことがあるから,$V_\text{in} \lt V_\text{out}$ である。
(2) $T_\text{on}$ の時間におけるリアクトルの電圧 $v_\text{L}$
リアクトルには電源の直流電圧 $V_\text{in}$ が直接印加される。よって,リアクトルの電圧 $v_\text{L}$ は,次式となる。
\[ v_\text{L}=V_\text{in}=L\frac{\text{d}i_\text{in}}{\text{d}t} \gt 0 \]したがって,電流 $i_\text{in}$ は増加する。
(3) $T_\text{off}$ の時間におけるリアクトルの電圧 $v_\text{L}$
デバイス S をオフしても電流は流れ続ける。ダイオード D が導通し,リアクトルの電圧 $v_\text{L}$ は,次式で求められる。
\[ v_\text{L}=V_\text{in} - V_\text{out} = L\frac{\text{d}i_\text{in}}{\text{d}t} \lt 0 \]したがって,電流 $i_\text{in}$ は減少する。
(4) ダイオード D に流れる電流 $i_\text{D}$ の平均値 $I_\text{D}$
電流 $I_\text{in}$ がダイオード D を流れるのはスイッチ S がオフの期間 $T_\text{off}$ だけであり,その大きさは $I_\text{in}$ である。スイッチ S がオンの期間 $T_\text{on}$ にダイオード D を流れる電流はゼロである。したがって,平均値 $I_\text{D}$ は,次式で求められる。
\[ I_\text{D}=I_\text{in} \times \frac{T_\text{off}}{T_\text{on}+T_\text{off}} \](5) 出力電圧 $V_\text{out}$
電源からチョッパへの入力電力 $V_\text{in} \times I_\text{in}$ と,チョッパから負荷への出力電力 $V_\text{out} \times I_\text{D}$ は等しい。また小問 (4) より,出力電圧 $V_\text{out}$ は,次式で求められる。
\[ V_\text{out}=V_\text{in}\times \frac{T_\text{on}+T_\text{off}}{T_\text{off}} \]問4 フィードバック制御系
図に示すフィードバック制御系について,次の問に答えよ。ここで,$R(s)$ は目標値,$E(s)$ は制御偏差,$Y(s)$ は制御量であり,$K \gt 0$ とする。
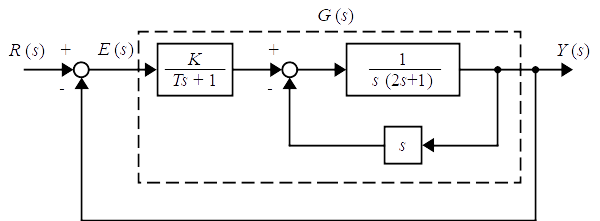
(1) 開ループ伝達関数 $\displaystyle G(s) = \frac{Y(s)}{E(s)}$ を求めよ。
(2) 閉ループ伝達関数 $\displaystyle W(s) = \frac{Y(s)}{R(s)}$ を求めよ。
(3) この制御系において,$T=0$ としたとき,閉ループ伝達関数 $W(s)$ の特性方程式は二次方程式となる。目標値のステップ状変化に対応する制御量の時間応答 $y(t)$ が振動的になる $K$ の条件を求めよ。
(4) 小問 (3) の制御系において $K=1$ としたとき,目標値の単位インパルス変化に対する制御量の時間応答 $y(t)$ を求めよ。
必要に応じて,ラプラス変換の複素領域における推移定理である $\mathcal{L}[e^{-at}x(t)] = X(s+a)$ を使ってよい。
(5) この制御系において,$T=2$ としたとき,閉ループ伝達関数 $W(s)$ の特性方程式は三次方程式となる。制御系を安定にする $K$ の条件をラウス・フルビッツの安定判別法を適用して求めよ。
問4 解答と解説
(1) 開ループ伝達関数 $G(s)$
$Y(s)$ は $E(s)$ を用いると次式で表される。
\[ Y(s)={\frac{K}{Ts+1}E(s)-sY(s)}\frac{1}{s(2s+1)} \]これを $Y(s)$ と $E(s)$ で整理する。
\[ s(2s+2)Y(s)=\frac{K}{Ts+1}E(s) \]開ループ伝達関数 $\displaystyle G(s) = \frac{Y(s)}{E(s)}$ は次式となる。
\[ G(s)=\frac{Y(s)}{E(s)}=\frac{K}{s(Ts+1)(2s+2)}=\frac{K}{2Ts^3+(2T+2)s^2+2s} \](2) 閉ループ伝達関数 $W(s)$
$Y(s)$ を $R(s)$ と $G(s)$ を用いて表す。
\[ Y(s)={R(s)-Y(s)}G(s) \]閉ループ伝達関数 $\displaystyle W(s) = \frac{Y(s)}{R(s)}$ は,次式となる。
\[ W(s)=\frac{Y(s)}{R(s)}=\frac{G(s)}{1+G(s)} \]上式に (1) で求めた $G(s)$ を代入する。
\[ Y(s)=\frac{\frac{K}{s(Ts+1)(2s+2)}}{1+\frac{K}{s(Ts+1)(2s+2)}} \] \[ Y(s)=\frac{K}{2Ts^3+(2T+2)s^2+2s+K} \](3) 制御量の時間応答 $y(t)$ が振動的になる $K$ の条件
閉ループ伝達関数 $W(s)$ に $T=0$ を代入する。
\[ W(s)=\frac{K}{2s^2+2s+K} \]制御系の系の特性方程式は次式のとおり,二次方程式となる。
\[ 2s^2+2s+K=0 \]目標値のステップ状変化に対応する制御量の時間応答 $y(t)$ が振動的になるのは,特性方程式の根が複素数になる場合である。すなわち,判別式 $D$ が $D \lt 0$ となる条件である。
\[ D=4-8K \lt 0 \]よって,$K$ の条件は $K \gt 0.5$ である。
(4) 目標値の単位インパルス変化に対する制御量の時間応答 $y(t)$
$K=1$ を $W(s)$ に代入する。
\[ W(s)=\frac{1}{2s^2+2s+1} \]目標値は単位インパルス関数なので,$R(s)=1$ であり,$Y(s)$ は,次式で求められる。
\[ Y(s)=R(s)W(s)=\frac{1}{2s^2+2s+1}=\frac{0.5}{s^2+s+0.5} \]上式を逆ラプラス変換することで,単位インパルス応答 $y(t)$ を得る。
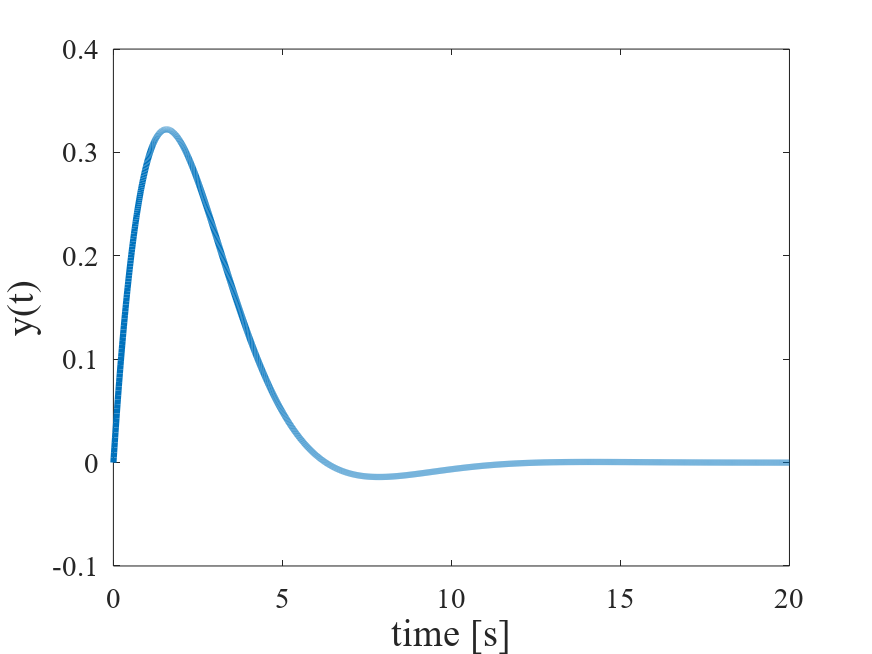
\[ y(t)=\mathcal{L}^{-1}[\frac{0.5}{s^2+s+0.5}] \] \[ y(t)=\mathcal{L}^{-1}[\frac{0.5}{(s+0.5)^2+0.5^2}] \] \[ y(t)=e^{-0.5t}\sin{0.5t} \](参考)目標値の単位インパルス変化に対する制御量の時間応答
目標値の単位インパルス変化に対する制御量の時間応答を下図に示す。
(5) 制御系を安定にする $K$ の条件
閉ループ伝達関数 $W(s)$ に $T=2$ を代入する。
\[ W(s)=\frac{K}{4s^3+6s^2+2s+K} \]閉ループ伝達関数 $W(s)$ の特性方程式は,次式の三次方程式となる。
\[ 4s^3+6s^2+2s+K=0 \]ラウス表は次表となる。
| $s^3$ 行 | 4 | 2 | 0 |
|---|---|---|---|
| $s^2$ 行 | 6 | $K$ | 0 |
| $s^1$ 行 | $\displaystyle \frac{12-4K}{6}$ | 0 | |
| $s^0$ 行 | $K$ |
このシステムが安定となる必要十分条件は,次式が成立することである。
\[ 12-4K \gt 0 \] \[ K \gt 0 \]上式より,$0 \lt K \lt 3$ を得る。