【要点ノート】自動制御及び情報処理【自動制御編】
はじめに
科目 Ⅱ 電気の基礎 問題 5 「自動制御及び情報処理」に関する要点ノートである。本稿では，以下の章立てで要点をまとめる。
自動制御編
情報処理編
自動制御系
制御（control）とは「ある目的に適合するように，対象となっているものに所要の操作を加えること」（JIS Z 8116 : 1994）と定められている。なお，目的としては，制御対象の特性を改善すること，その特性の変動を相殺すること，外乱など制御対象に外部から加わる好ましくない影響を相殺すること，制御量を目的値に近づけること，又は追従させること，などがある。
自動制御の歴史
産業革命の原動力となったワットの蒸気機関は余りにも有名であるが，それを支えた制御技術として目標の回転速度を維持するガバナ（遠心調速機）があることは，余り知られていない。
ガバナとは，負荷が小さくなって回転速度が上昇すると，遠心錘に遠心力が作用して弁の開度が小さくなる仕組みである。回転速度が下降すると逆の減少が起こる。これは正にフィードバック制御の原理そのものである。
やがて速度制御の精度向上の要求に対処するため，技術者達は遠心錘の感度を高くすることに腐心した。現在の制御系の言葉でいえば，利得を大きくすることに相当する。しかし，そのような改良では系は振動的となり，ついには不安定となることが分かってきた。
この点を解決するために，電磁気学で有名なマクスウェルは，速度制御の精度向上は遠心錘の改良だけでは不十分であり，制御系全体としての微分方程式を導き，その安定性を議論しなければならないことを説いて，系が安定であるためには特性方程式のすべての根が負の実数部を持たなければならないことを示した。彼は，三次系については安定性の必要十分条件を導いた。しかし，制御系に積分動作を持たせるなどして系の次数が更に高くなった場合については，完全に解くことができなかった。
1950 年代に入ると，それまでの古典制御に代わって，時間領域で多入出力系の取り扱いを特徴とする状態空間法が生まれ，現代制御理論と呼ばれた。この新しい制御理論は，制御対象の正確なモデルを必要としたため，現場の技術者に嫌われ，ここにいわゆる「理論と現実の乖離」が生じた。
このような反省から，1990 年代になると，両者を包括する新しい理論としてロバスト制御（robust control）[1]が生まれた。
- 制御系の設計は制御対象のモデルに基づいて行われるが，モデルには非線形性や寄生容量の無視，パラメータ変動などに起因する不確かさが含まれている場合が多い。モデルに含まれる不確かさを許容し，粗い近似モデルに基づく制御でも性能が保証できるような配慮を加えた制御をロバスト（頑健な）制御と呼ぶ。ロバスト制御の手法としては H ∞ 制御，二次安定化，構造化特異値構成，パラメトリックな安定化手法などがあげられる。ロバスト制御は理論の実用的価値を著しく高め，制御工学における理論と実際のギャップを少なくするのに貢献した。（出典）機械工学辞典
自動制御系の分類
自動制御（automatic control）とは「制御系を構成して自動的に行われる制御」（JIS Z 8116 : 1994）である。制御信号の流れからフィードバック制御（feedback control），フィードフォワード制御（feedfoward control），シーケンス制御（sequential control）に分類できる。
| 制御方式 | 内容 |
|---|---|
| フィードバック制御 | 出力結果と目標値とを比較して，一致するように制御を行う |
| フィードフォワード制御 | 外乱を予測して，影響が生じる前に機器の動作を制御する |
| シーケンス制御 | 決められた手順や条件に従って，逐次的に制御の段階を進める |
フィードバック制御（feedback control）
フィードバック制御系の標準的な形を下図に示す。また，フィードバック制御系の基本回路構成に関する用語の説明も記す。
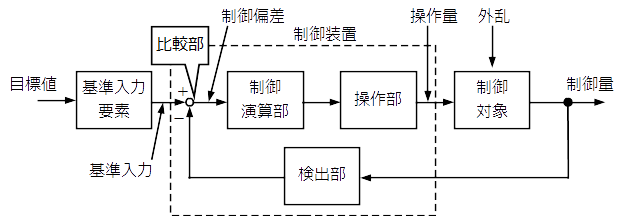
- 制御量（controlled variable）
- 制御対象に属する量のうちで，それを制御することが目的となっている量
- 目標値（desired value, command）
- 制御系において，制御量がその値を取るように目標として与えられる量
- 制御偏差（deviation, error）
- 目標値と制御量の差
- 操作量（manipulated variable, control input）
- 制御系において，制御量を制御するために制御対象に加える量
- 外乱（disturbance）
- 制御系の状態を乱そうとする外部からの作用
- 制御対象（controlled object）
- 制御の対象となる系で，機械，プロセス，プラントなどの全体または一部がこれに当たる
- 制御装置（controller, control device）
- 検出部，比較部，制御演算部からなり，操作量を生成する装置
- 比較部（comparing element）
- 制御装置において，目標値と，制御量または制御対象からフィードバックされる信号とを比較する部分
- 制御演算部（controlling element）
- 制御装置において，目標値に基づく信号および検出部からの信号を基にして，制御系が所要の働きをするのに必要な信号を作り出して操作部へ送出す部分
- 操作部（final controlling element）
- 制御装置において，制御演算部などからの信号を操作量に変えて，制御対象に働きかける部分
- 検出部（detecting element）
- 制御装置において，制御対象，環境などから制御に必要な信号を取り出す部分
制御系の分類
制御系にはいろいろな種類があり，その分類の方法も多様である。
まず，目標値の種類による分類として定値制御と追値（追従）制御がある。定値制御は目標値が一定の場合で，そこでは外乱の抑制制御が重要である。例えば，恒温槽の温度制御，発電機の出力電圧制御などがこの例である。これに対し，追値（追従）制御では，目標値が任意に変化し，それを正確に追うことが主な目的となる。XY プロッタ，レーダの自動追尾装置，工作機械などがその好例である。
次に，制御量の種類による分類として，制御量が温度，圧力，流量，濃度などであるプロセス制御，制御量が物体の位置，回転角，姿勢などであるサーボ機構などがある。
開放システム
システム理論の文脈でよく使われる「サイバネティクス」という理論における「開放システム」がフィードバック制御である。開放システムとは，システムとして外部と通信（やりとり）をすることで体をなしている状態のことをいう。世の中のほとんどのものは開放システムとして成り立つ。
開放システムを構造化すると，入力（インプット） → システム処理 → 出力（アウトプット）という構造が成り立つ。出力結果からのフィードバックを経て，入力を制御することや調整することがある。フィードバックには正（＋）と負（－）があり，それぞれ促進（＋）と抑制（－）を意味し，入力（インプット）を制御する。
正のフィードバック（促進，ポジティブフィードバック，positive feedback）とは，人間でいえば運動しているときにアドレナリンをずっと分泌し続け，疲れや痛みが感じにくくなる状態で，通常のシステムとしては破壊行為に等しいため，長続きしない。一方，負のフィードバック（抑制，ネガティブフィードバック，negative feedback）とは，アドレナリンがずっと分泌され続けている体の限界を見定めて抑制することで，人間としてのシステムを維持する。この正と負のフィードバックをうまく組み合わせて，円滑にループさせていくことで，システムとしてのダイナミクス（動力学）が生まれる。
フィードフォワード制御（feedfoward control）
フィードフォワード制御とは「目標値，外乱などの情報に基づいて，操作量を決定する制御」である。
一般の開ループ制御は，外乱の影響を考慮する必要のない操作量と制御量に一意的対応の付く制御対象に対して行われる制御であるが，外乱の影響を受ける制御対象に対して，外乱の情報によってその影響が制御系に現れる前に前もって訂正動作を行う制御をいう。
シーケンス制御（sequential control）
シーケンス制御とは「あらかじめ定められた順序又は手続きに従って制御の各段階を逐次進めていく制御」である。自動販売機，券売機，エレベータなどはシーケンス制御により動作している。
最適制御（optimal control, optimum control）
最適制御とは「制御過程又は制御結果を，与えられた基準に従って評価し，その評価成績を最も良くする制御」である。
適応制御（adaptive control）
システムの動特性の変化に対して，制御パラメータの種類若しくは大きさ，又はその両方を変化させ，常に適切な状態で制御を行う制御手法。
この制御手法では，複雑な演算を行うが，システム内のあいまいさを同定し，パラメータ固定制御では扱えないような大きな特性変化に対しても用いられる。
要素と伝達関数
伝達関数（transfer function）は次の式で定義される。
伝達関数とは，動的システムの特性において，すべての初期値を 0 とした特性の別表現であるといえる。
制御対象の伝達関数の分母が $s$ に関して 1 次多項式となる場合，その対象を 1 次遅れ系（first order system），2 次多項式となる場合，その対象を 2 次遅れ系（second order system）と呼ぶ。また，「入力から出力までの伝達関数は・・・」という表現を使うことが多い。
1 次遅れ系
1 次遅れ系の一般形の伝達関数 $G(s)$ は，次式で表される。
\[ G(s)=\frac{b}{s+a}=\frac{K}{Ts+1} \]ただし，$\displaystyle T=\frac{1}{a} \gt 0$，$K=\frac{b}{a} \gt 0$ である。システムの応答を考える際には，$\displaystyle G(s)=\frac{K}{Ts+1}$ の表現を使った方が都合がよい。
2 次遅れ系
2 次遅れ系の伝達関数の一般形は，次式で表される。
\[ G(s)=\frac{K{\omega_\text{n}}^2}{s^2+2\zeta\omega_\text{n}s+{\omega_\text{n}}^2} \]ただし，減衰比 $\zeta \gt 0$，固有角周波数 $\omega_\text{n} \gt 0$ である。2 次遅れ系では，1 次遅れ系の場合と異なり，伝達関数 $G(s)$ の分母が $s$ に関して 2 次多項式であるため，応答の計算には注意する必要がある。
制御理論の基礎
ブロック線図と伝達関数
ブロック線図（block diagram）とは「システムを構成する要素間の信号伝達による結合関係を表現する線図」（JIS Z 8116 : 1994）である。
ブロックに入る矢印を表す変数を入力，ブロックから出る矢印を表す変数を出力とみなせば，数式の説明とブロック線図の対応づけがわかる。ブロック線図における矢印を一般に，ブロックへの入力信号（input signal），出力信号（output signal）と呼ぶことが多い。
ブロック線図の基本図形は以下の 3 つの要素で作成される。
ブロック
ブロックと呼ばれる長方形の中に系の伝達関数 $G(s)$ を書き込み，入力信号 $X(s)$ と出力信号 $Y(s)$ を表す矢印を付ける。この図の場合，$Y(s) = G(s)X(s)$ を表している。
加え合わせ点
下図は加え合わせ点といわれ，2 つの入力 $X(s)$ と $Y(s)$ の加減算 $X(s) \pm Y(s)$ を表している。○に向かう信号には，＋または－の符号を付けて，入力信号が加算または減算されることを示す。
引き出し点
下図の引き出し点は，必要に応じて同一信号を任意に引き出せることを意味している。
ラプラス変換（Laplace transformer）
ラプラス変換により，ある種の微分・積分は，積などの代数的な演算に置き換わるため，制御工学などにおいて，時間領域の関数を別の領域に変換することにより，計算方法の見通しを良くすることができる。
計算方法の見通しを良くする，を具体的に言えば，微分方程式を代数方程式に変形し，簡単に解くことのできる便利なツールである。
実数 $t \ge 0$ について定義された関数 $f(t)$ のラプラス変換は，次式で定義される。
\[ F(s) =\mathcal{L}[f(t)]= \int^{\infty}_{0} f(t) e^{-st}dt \]ここで，$s$ は複素数であり，2 つの実数，$\sigma$，$\omega$ を用いて，$s = \sigma + j\omega$ と表すことができる（$j$ は虚数単位）。要するに，「時間 $t$ で変化する関数 $f(t)$ を複素数 $s$ で変化する関数 $F(s)$ に変換する」ということである。
また，$c \gt 0$ として，関数 $F(s)$ から元の関数 $f(t)$ を計算することを逆ラプラス変換（inverse Laplace transform）といい，次式で定義される。
\[ f(t) = \mathcal{L}^{-1}[F(s)]=\lim_{p \to \infty} \frac{1}{2\pi j}\int^{c + jp}_{c - jp} F(s) e^{st} ds \]| 関数 | $f(t)$ | $F(s)$ |
|---|---|---|
| デルタ関数（delta function） | $\delta (t)$ | $1$ |
| 単位ステップ関数（unit step function） | $u (t)$ | $\displaystyle \frac{1}{s}$ |
| 単位ランプ関数（unit Ramp function） | $t$ | $\displaystyle \frac{1}{s^2}$ |
| 指数関数（exponential function） | $e^{-\alpha t}$ | $\displaystyle \frac{1}{s + \alpha}$ |
| $t e^{-\alpha t}$ | $\displaystyle \frac{1}{(s + \alpha)^2}$ | |
| $t^n e^{-\alpha t}$ | $\displaystyle \frac{n!}{(s + \alpha)^{n+1}}$ | |
| 正弦関数（sine function） | $\sin\omega t$ | $\displaystyle \frac{\omega}{s^2 + \omega^2}$ |
| 余弦関数（cosine function） | $\cos\omega t$ | $\displaystyle \frac{s}{s^2 + \omega^2}$ |
| $e^{-\alpha t}\sin\omega t$ | $\displaystyle \frac{\omega}{(s+\alpha)^2 + \omega^2}$ | |
| $e^{-\alpha t}\cos\omega t$ | $\displaystyle \frac{s+\alpha}{(s+\alpha)^2 + \omega^2}$ | |
| $\displaystyle \frac{t^n}{n!}$ | $\displaystyle \frac{1}{s^{n+1}}$ |
過渡応答（transient response）
系に加えられる入力がある定常状態（steady state）から別の定常状態に変化したとき，出力が変化後の定常状態に達するまでの応答を過渡応答（transient response）という。一般に，過渡応答には次のものが用いられる。
インパルス応答（impluse response）
インパルス入力が加わったときの応答をインパルス応答という。特に，入力が単位インパルス関数である場合，単位インパルス応答という。
インパルス応答の計算法
伝達関数を用いてインパルス応答を求めてみる。まず，つぎの微分方程式を考える。（この微分方程式は，$RL$ 回路の特性やモータの特性を一般化したものである。）
\[ \frac{\text{d}y(t)}{\text{d}t}+ay(t)=bu(t) \]上式の両辺を各時間変数の初期値をすべて 0 としてラプラス変換すると，次式が得られる。
\[ (s+a)Y(s)=bU(s) \]ここで，$U(s)$ と $Y(s)$ は，それぞれ $u(t)$，$y(t)$ のラプラス変換である。$U(s)$ を入力信号，$Y(s)$ を出力信号としたとき，システムの伝達関数は $G(s)$ は，次式となる。
\[ G(s)=\frac{Y(s)}{U(s)}=\frac{b}{s+a} \]前述のとおり，逆ラプラス変換によって独立変数 $s$ の関数を時間変数 $t$ の関数に戻すことができる。よって，出力の時間変数 $y(t)$ は，次式で求められる。
\[ y(t)=\mathcal{L}^{-1}[F(s)]=\mathcal{L}^{-1}[G(s)U(s)] \]上式は，「システムの時間応答は，伝達関数 $G(s)$ と入力信号のラプラス変換 $U(s)$ の積を逆ラプラス変換することで求められる」ことを示している。さらに，$G(s)$ や入力信号 $U(s)$ を特定していないので，1 次遅れ系のインパルス応答の計算以外でも成り立つ。
ここで，インパルス応答のラプラス変換 $U(s)=\mathcal{L}^{-1}[\delta(t)]=1$ より，出力の時間変数 $y(t)$ は，次式となる。
\[ y(t)=\mathcal{L}^{-1}[G(s)U(s)]=\mathcal{L}^-1[\frac{b}{s+a}\times 1]=b\mathcal{L}^{-1}[\frac{1}{s+a}]=be^{-at} \]この結果は，微分方程式により求めた結果と同じになり，しかも煩雑な積分計算を行う必要がない。また，上式よりインパルス応答を求めるときは伝達関数 $G(s)$ そのものを逆ラプラス変換すればよいことがわかる。
ここで，前述のようにシステムの応答を考える際には，$\displaystyle G(s)=\frac{K}{Ts+1}$ の表現を使ったほうがよいので，インパルス応答は次式のように表せる。
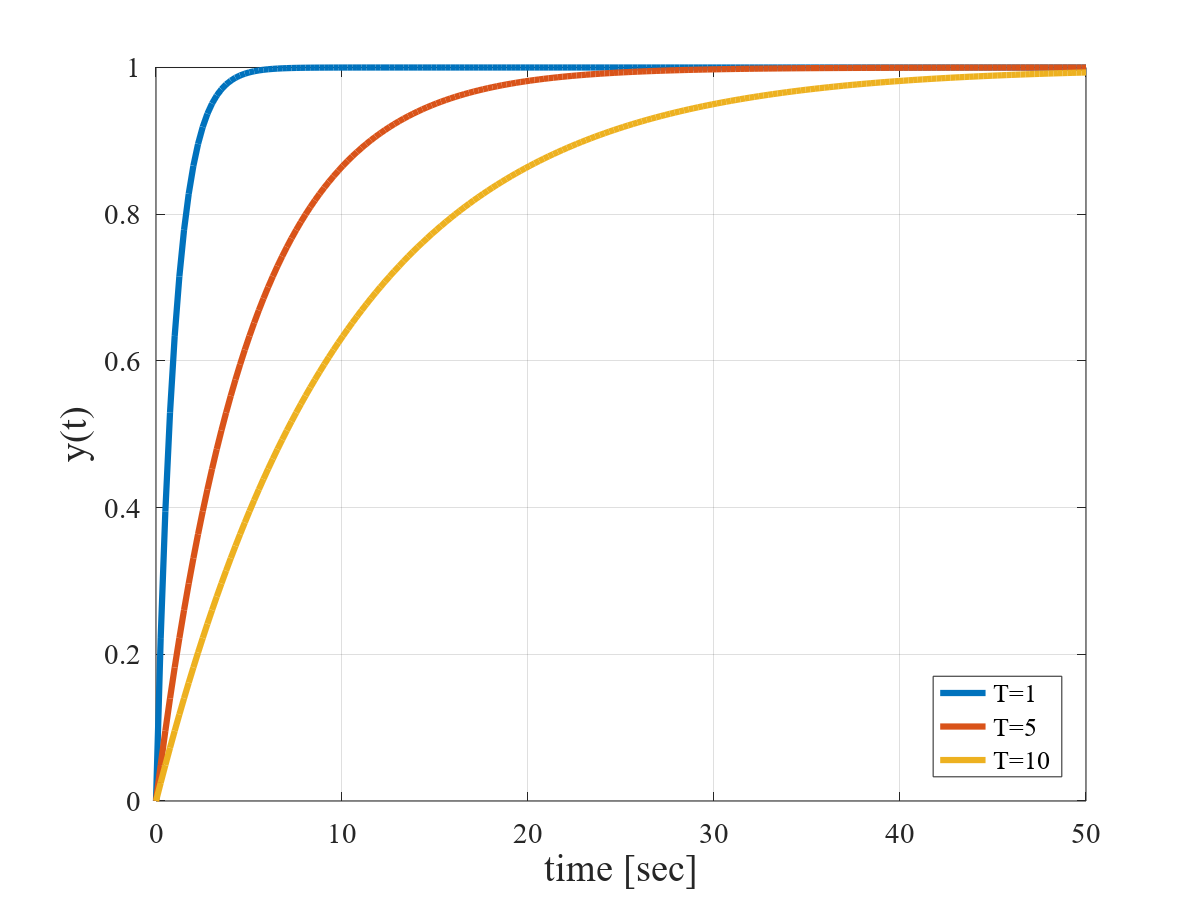
\[ y(t)=\frac{K}{T}e^{-\frac{1}{T}t} \]指数関数の性質により，$y(t)$ の初期値（$t=0$ のときの値）は，$\displaystyle y(0)=\frac{K}{T}$ である。また，$T \gt 0$ であるので，指数関数のべき指数の部分 $\displaystyle -\frac{1}{T}t$ は必ず負の値となる。$K=T$ の場合のインパルス応答を描くと，次の図のようになる。下図より，$T$ が大きくなるにしたがい，インパルス応答が 0 に収束するのに時間がかかることがわかる。
ステップ応答（step response）
ステップ入力が加わったときの応答をステップ応答という。特に入力が単位ステップ（単位関数 $u(t)$ で表される）である場合，単位ステップ応答（unit step response）あるいはインディシャル応答（indicial response）と呼ばれる。
一般に，応答特性の評価基準に，ステップ応答が用いられることが多い。その理由はステップ入力が実現しやすく，実験的に応答試験ができること，過渡的な性質を十分表していることである。
ステップ応答の計算法
単位ステップ信号 $u_\text{s}(t)=1$ のラプラス変換 $\displaystyle U(s)=\frac{1}{s}$ を用いて，出力の時間変数 $y(t)$ を求める。ただし，システムの伝達関数 $G(s)$ は，インパルス応答を計算したときと同様に，$\displaystyle G(s)=\frac{b}{s+a}$ とした。
\[ y(t)=\mathcal{L}^{-1}[G(s)\times\frac{1}{s}]=\mathcal{L}^{-1}[\frac{b}{s(s+a)}]=\mathcal{L}^{-1}[\frac{b}{a}(\frac{1}{s}-\frac{1}{s+a})] \] \[ y(t)=\frac{b}{a}(1-e^{-at}) \]ここで，前述のようにシステムの応答を考える際には，$\displaystyle G(s)=\frac{K}{Ts+1}$ の表現を使ったほうがよいので，ステップ応答は次式のように表せる。
\[ y(t)=K(1-e^{-\frac{1}{T}t}) \]$K=1$ の場合のステップ応答を描くと，次の図のようになる。$T$ の値が大きくなるにしたが，定常値（$K=1$）に収束するまでに時間がかかることがわかる。
ランプ応答（ramp response）
時間 $t \lt 0$ の区間では $x(t) = 0$ であり，$t \gt 0$ で $x(t) = at$ （$a$ は定数）である時間関数をランプ関数といい，ランプ関数状入力を単にランプ入力という。ランプ入力が加わったときの応答をランプ応答という。
2 次遅れ系の応答
2 次遅れ系のインパルス応答の計算
2 次遅れ系の伝達関数の一般形は次式で表される。
\[ G(s)=\frac{K{\omega_\text{n}}^2}{s^2+2\zeta\omega_\text{n}s+{\omega_\text{n}}^2} \]ただし，減衰比 $\zeta \gt 0$，固有角周波数 $\omega_\text{n} \gt 0$，$K$ は定数である。
インパルス応答は 1 次遅れ系の場合と同様に，伝達関数 $G(s)$ を逆ラプラス変換して求める。2 次遅れ系の伝達関数の一般形を次のとおり部分分数に分解する。
\[ G(s)=\frac{K{\omega_\text{n}}^2}{s^2+2\zeta\omega_\text{n}s+{\omega_\text{n}}^2}=\frac{K{\omega_\text{n}}^2}{(s-\alpha)(s-\beta)}=\frac{k_1}{s-\alpha}+\frac{k_2}{s-\beta} \]上式より，$\alpha$，$\beta$ は方程式 $s^2+2\zeta\omega_\text{n}s+{\omega_\text{n}}^2=0$（$G(s)$ の「分母多項式」= 0）の根，すなわち極であることがわかる。方程式を解くと，根 $\alpha$，$\beta$ が求められる。
\[ \alpha, \beta = -\zeta\omega_\text{n}\pm\sqrt{\zeta^2{\omega_\text{n}}^2-{\omega_\text{n}}^2}=-\zeta\omega_\text{n}\pm\sqrt{\zeta^2-1} \omega_\text{n} \]ここで，根 $\alpha$，$\beta$ は，$\zeta \gt 0$ がとる値によって，つぎの 3 つに分類できる。
- $0 \lt \zeta \lt 1$ の場合：$\alpha$，$\beta$ は共役複素数
- $\zeta = 1$ の場合：$\alpha = \beta$ となる重根（実数）
- $\zeta \gt 1$ の場合：$\alpha$，$\beta$ は異なる 2 つの実数根
したがって，$\zeta$ の値により場合分けをして考える必要がある。
$0 \lt \zeta \lt 1$ の場合
2 次遅れ系の曲は，次式の共役複素数で与えられる。
\[ \alpha, \beta =-\zeta\omega_\text{n}\pm\text{j}\sqrt{1-\zeta^2} \omega_\text{n} \]部分分数分解による方法を用いてインパルス応答を計算することもできるが，別の方法で計算する。まず，$G(s)$ を次式のように変形する。
\[ G(s)=\frac{K{\omega_\text{n}}^2}{s^2+2\zeta\omega_\text{n}s+{\omega_\text{n}}^2} =\frac{K{\omega_\text{n}}^2}{(s+\zeta\omega_\text{n})^2-\zeta^2{\omega_\text{n}}^2+{\omega_\text{n}}^2} \] \[ G(s)=\frac{K{\omega_\text{n}}^2}{(s+\zeta\omega_\text{n})^2+(1-\zeta^2){\omega_\text{n}}^2} \] \[ G(s)=\frac{K\omega_\text{n}}{\sqrt{1-\zeta^2}}\frac{\sqrt{1-\zeta^2}\omega_\text{n}}{(s+\zeta\omega_\text{n})^2+(\sqrt{1-\zeta^2}\omega_\text{n})^2} \]上式を逆ラプラス変換すると，インパルス応答 $y(t)$ が求められる。
\[ y(t)=\mathcal{L}^{-1}[\frac{K\omega_\text{n}}{\sqrt{1-\zeta^2}}\frac{\sqrt{1-\zeta^2}\omega_\text{n}}{(s+\zeta\omega_\text{n})^2+(\sqrt{1-\zeta^2}\omega_\text{n})^2}] \] \[ y(t)=\frac{K\omega_\text{n}}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_n t}\sin{\sqrt{1-\zeta^2}\omega_\text{n}t} \]$\zeta = 1$ の場合
このとき，2 次遅れ系の伝達関数 G(s) は，次式で表される。
\[ G(s)=\frac{K{\omega_\text{n}}^2}{s^2+2\omega_\text{n}s+{\omega_\text{n}}^2}=\frac{K{\omega_\text{n}}^2}{(s+\omega_\text{n})^2} \]したがって，2 次遅れ系の極は，$\alpha = \beta =-\omega_\text{n}$ の重根で与えられる。ラプラス変換表よりインパルス応答 $y(t)$ は，次式で表される。
\[ y(t)=\mathcal{L}^{-1}[\frac{K{\omega_\text{n}}^2}{(s+\omega_\text{n})^2}]=K{\omega_\text{n}}^2 t e^{-\omega_\text{n}t} \]$\zeta \gt 1$ の場合
2 次遅れ系の極は異なる 2 つの実数根で与えられる。いま，$\alpha=-\zeta\omega_\text{n}+\sqrt{\zeta^2-1}\omega_\text{n}$，$\beta=-\zeta\omega_\text{n}-\sqrt{\zeta^2-1}\omega_\text{n}$ とすると，2 次遅れ系の伝達関数 G(s) は，次式で表される。
\[ G(s)=\frac{K{\omega_\text{n}}^2}{s^2+2\zeta\omega_\text{n}s+{\omega_\text{n}}^2}=K(\frac{k_1}{s+\zeta\omega_\text{n}-\sqrt{\zeta^2-1}\omega_\text{n}}+\frac{k_2}{s+\zeta\omega_\text{n}+\sqrt{\zeta^2-1}\omega_\text{n}}) \]未知定数 $k_1$ と $k_2$ は次式となる。（求める過程は省略）
\[ k_1=\sqrt{\omega_\text{n}}{2\sqrt{\zeta^2-1}} \] \[ k_2=-k_1=-\sqrt{\omega_\text{n}}{2\sqrt{\zeta^2-1}} \]インパルス応答 $y(t)$ は，次式で表される。
\[ y(t)=\frac{K\omega_\text{n}}{2\sqrt{\zeta^2-1}}\{e^{(-\zeta\omega_\text{n}+\sqrt{\zeta^2-1}\omega_\text{n})t}-e^{(-\zeta\omega_\text{n}-\sqrt{\zeta^2-1}\omega_\text{n})t}\} \]インパルス応答の解析
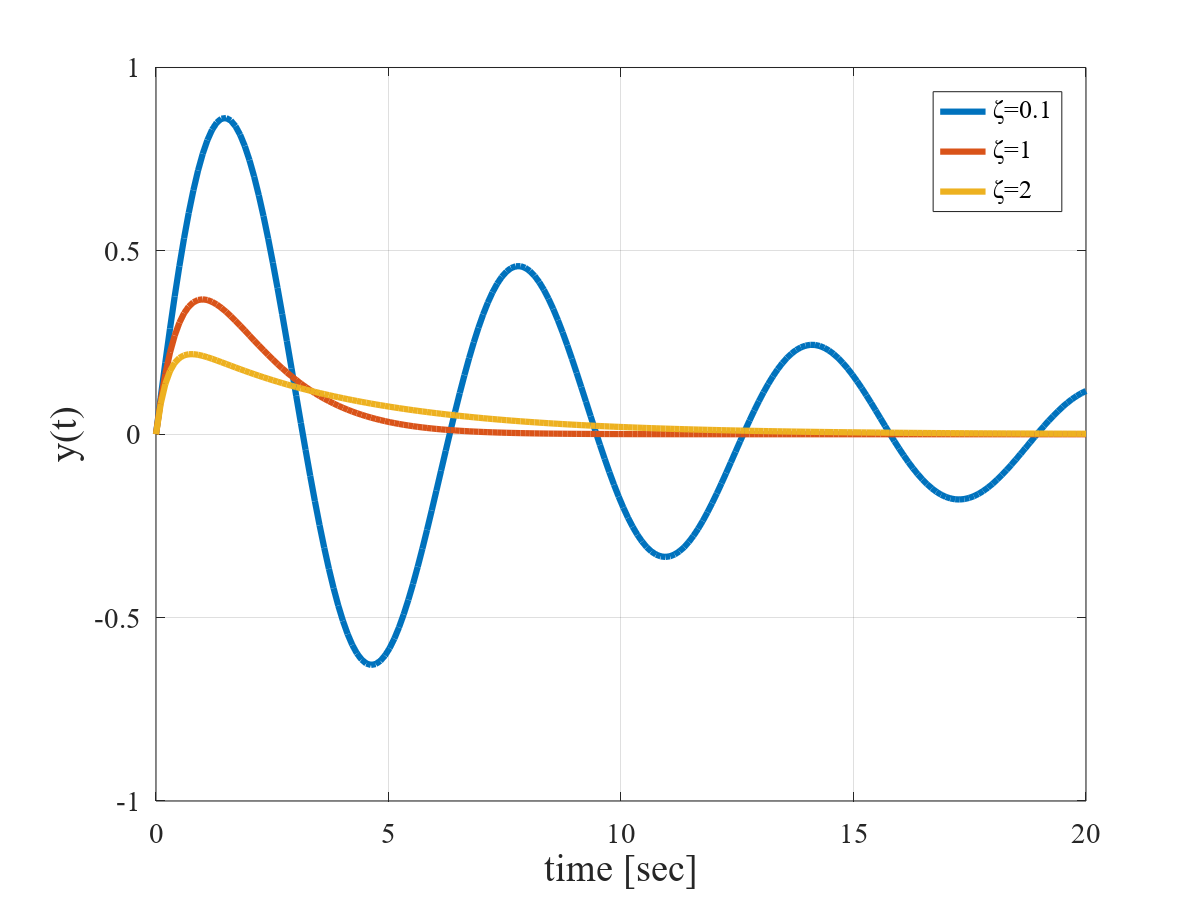
例として，$\zeta=0.1$（$0 \lt \zeta \lt 1$），$\zeta=1$ 及び $\zeta=2$（$\zeta \gt 0$）とし，$\omega_\text{n}=1$，$K=1$ とした場合のインパルス応答を下図に示す。
制御系の安定判別
安定な制御系であるためには次のことが必要である。
- 目標値を変更したときは，制御量は新しい目標値に追従し，偏差は無限に大きくならず，一定に近づく。
- 外乱が加わったときは，一時的に系の状態が乱されても再びもとの状態の近くに回復する。
このようなことがらをまとめ，自動制御系の安定性（stability）を次のように定義することができる。
「入力や外乱によって発生する過渡現象が時間とともに減衰する系を安定（stable）な系，逆に発散する系を不安定（unstable）な系，一定振幅で振動を持続する系を安定限界である系という。」
システムの安定性
有界なすべての（種類の）入力に対して，システムの応答が発散しない（応答が有界）場合，「安定（stable）」であると呼び，そうでない場合は「不安定（unstable）」であると呼ぶ。
定常特性
制御系の時間応答は，過渡応答と定常応答に分けて考えることができる。過渡応答が定常状態（steady-state）に落ち着くまでの変動的な応答であるのに対し，定常応答（steady state response）は入力の定常状態の変化に応じた出力の定常状態の変化である。実際の制御系では入力または外乱が変化した後，すぐに過渡応答成分が消え，定常応答成分だけが残るが，数学的には時間 $t \to \infty$ として求める。いま，系の出力を $y(t)$ とし，$y(t)$ の定常状態に達したときの値を $y_{ss}$ とすれば，次式が成り立つ。
\[ y_{ss} = \lim_{t \to \infty} y(t) \]下図のように，伝達関数が $W(s)$ である系の単位ステップ応答では，入力が $X(s) = 1/s$ であるから，$Y(s)$ は次式で求められる。
\[ Y(s) = W(s) \cdot \frac{1}{s} \]
これにラプラス変換の最終値の定理を用いれば，逆変換しなくても伝達関数から $y_ss$ が直接求められる。
\[ y_{ss} = \lim_{t \to \infty} y(t) = \lim_{s \to 0} sY(s) = \lim_{s \to 0} W(s) \]最終値の定理（final value theorem）
最終値の定理が使える条件は，システム $sF(s)$ の極の実部がすべて負となることである。
\[ \lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s) \]PID 制御系とフィードバック制御系の分類
PID 制御系
PID 動作（proportional-plus-integral-plus-derivative control）とは，比例（proportional），積分（integral），微分（derivative）すべての動作を含めた動作で，伝達関数は次のように表される。
\[ G_c (s) = K_p (1 + \frac{1}{T_I s} + T_D s) \]$K_p$，$T_I$，$T_D$ を適当な値に設定することで，最適な動作を実現できる。ここで，$K_p$ は定数で，比例ゲイン（proportional gain）（P ゲイン）と呼ばれる。
例えば，比例要素のあるフィードバック制御系の制御において，定値制御における定常偏差をなくすためには，制御器に積分要素を加えることが有効であり，過渡時に振動を抑制し素早く目標値に追従するためには，制御器に微分要素を加えることが有効である。
比例制御（proportional action）
比例制御とは「入力に比例する大きさの出力を出す制御」である。P 動作と略称することもある。
積分動作（integral action ; reset action）
積分動作（リセット動作）とは「入力の時間積分値に比例する大きさの出力を出す制御動作」である。I 動作と略称することもある。
微分制御（derivative action）
微分制御とは「入力の時間微分値に比例する大きさの入力を出す制御動作」である。D 動作と略称することもある。D 制御は偏差 $e(t)$ が，$t=t_0$ からごく近い未来にどのように変化するかという情報を使い，偏差の絶対値が増加（減少）しつつあるときは，操作量の絶対値 $|u_d (t)|$ を増やす（減らす）制御である。フィードバック制御系が安定に設計されていれば，偏差の未来（の近似）情報を用いる D 制御は，偏差の絶対値が課題になることを防ぐ役割を果たし，結果的に制御系の過渡特性を改善することに役立つ。
フィードバック制御系の分類
目標値の状態，制御量の種類による 2 つの分類とそれによる種類を取り上げる。
目標値による分類
フィードバック制御は目標値の状態により，定置制御と追従制御の 2 つに分類できる。
- 定置制御（set-point control）
- 目標値が一定である制御
- 追従制御（follow-up control, tracking control）
- 目標値が変化する制御。さらに，プログラム制御（program control）とサーボ制御（servo system）に分類できる。
制御量による分類
制御量の種類により，自動調整，サーボ機構，プロセス制御の 3 つに分類できる。
- 自動調整（automatic regulation）
- 原動機や電動機の調速，電圧調整，周波数制御等に用いられる制御
- サーボ機構（servomechanism）
- 兵器の自動照準，航空機の自動操縦，工作機械のならい制御等で発達した制御系であって，主として制御量は位置である
- プロセス制御（process control）
- 主として化学工業の分野で発達した制御であり，工業プロセスの状態に関する諸量，例えば温度，圧力，流量，液位，組成，品質，効率などの制御である
フィードバック制御系では，制御量を目標値に一致させるような制御動作が常に働いている。追従制御系においては，目標値が時々刻々変化していて，変化が激しい場合には制御量が目標値から離れる場合もある。また，定値制御系であっても，予想できない外乱が加わり，そのために制御量が乱されることもある。
一般に，目標値や外乱の変化の様態は千差万別であり，しかも予想し難いことが多い。そこで，制御系の応答特性を表すのに，定まった形状のテスト信号を入力信号として系に加え，それに対する出力信号の応答を用いる方法がとられる。これには周波数応答と過渡応答がある。
周波数応答（frequency response）
下図のように，線形かつ安定な系 $G(s)$ に振幅 $A$，角周波数 $\omega$ [rad/s] の正弦波 $x(t) = A \sin \omega t$ が入力として加わるものとする。正弦波入力が加わった直後には出力に過渡的な乱れが生じるが，安定な系であれば過渡応答成分はやがて消滅し，後には定常的な正弦波信号だけが残る。すなわち，定常状態に達してからの出力は $y(t) = B\sin(\omega t + \phi)$ と表される。このように系に正弦波入力を加えたときの出力の定常状態における応答を周波数応答（frequency response）という。
系が線形であれば，出力も入力と同じ周波数の正弦波となり，両者の差異は振幅 $A$ と $B$ が異なること，および，位相のずれ $\phi$ が生じることの 2 つである。そこで，周波数応答（出力の入力に対する関係）を表すのに，振幅の比 $B/A$ と位相のずれ $\phi$ を用いる。振幅比 $B/A$ のことをゲイン（gain）と呼び，位相のずれ $\phi$ を単に位相（phase）と呼んでいる。
ここで，角周波数 $\omega$ を変化させると，ゲインと位相は $\omega$ の値に応じて変化する。ゲインと位相が $\omega$ とどのような関数関係にあるかを示す特性を周波数特性（frequency characteristics）という。
伝達関数が $G(s)$ である系の周波数応答は，$G(s)$ の $s$ を $j\omega$ で置き換えた $G(j\omega)$ によって表される。この $G(j\omega)$ のことを周波数伝達関数（frequency transfer function）という。
ゲイン線図
ゲイン線図を描いて周波数解析を行うことがある。
ゲイン線図は，角周波数を $\omega$，周波数伝達関数を $G(\text{j}\omega)$ として，横軸に $\log_{10}{\omega}$，横軸にゲインにデシベル値 $20\log_{10}{|G(\text{j}\omega)|}$ をとって表すグラフである。
1 次遅れ系の周波数応答
例として，安定な 1 次遅れ系
\[ G(s) =\frac{K}{Ts+1} \]の周波数応答を求める。（$T \gt 0$，$K \gt 0$）
1 次遅れ要素（first order element）の周波数特性は，次式で表される。
\[ y(t)=\frac{K}{\sqrt{(\omega T)^2 +1}}A\sin{(\omega t -\tan^{-1}{\omega T})} \]ここでは，$K=1$ として，$T$ の値を変化させた場合を考える。$T$ が 0.01，1，100 のときの周波数応答のボード線図を下図に示す。
2 次遅れ系の周波数応答
次式に示す 2 次遅れ系の周波数応答を求める（分母は 2 次，分子は 0 次）。
\[ G(s)=\frac{K}{(T_1 s + 1)(T_2 + 1)} \]$\omega$ → 大（$+\infty$）としたとき，大きさは 0，ゲインは -40 [dB/dec]，位相は -180 ° となる。
一例として，二次遅れ系 $\displaystyle P(s) = \frac{10}{(s+1)(s+10)}$ について考えてみる。このときのゲイン線図では，直流ゲインの値は 0 [dB] であり，高周波帯域では傾きが -40 [dB/dec] のグラフになる。ここで，dec は対数スケールで 10 倍比を表す単位である。
ボード線図に関する補足
現実のシステムに直面した場合，$RC$ 回路のように回路の基本特製はわかるが，具体的な $R$ や $C$ の値はわからないことが多い。そこでシステムの周波数応答により，ボード線図が描ければ，それから折れ点接点がわかり，$T$ の値が決定できる。また，ゲインが一定値となる部分の値を読み取ることで $K$ の値がわかり，具体的な $R$ と $C$ の値が決定できる。このように，システムの応答から物理パラメータの具体的な値を決定することをパラメータ同定（parameter identification）と呼ぶ。
システムのアナロジー
機械系のモデルでも電気系のモデルでも微分方程式が同じ形式であれば，伝達関数は同じ形式となる。このような性質を，類似（アナロジー : analogy）という。制御工学の適用範囲は工学全般にわたるため，アナロジーの性質は非常に重要である。いいかえると，機械系の制御，電気電子系の制御ではなく，一般系としての制御工学があり，その中身を理解しておけばどのようなシステムでも関係なく，制御工学の知識が適用可能である。
機械系（直線運動と回転運動），電気系，熱系のアナロジーを下表にまとめる。特定のシステムを意識せず，一般形で解析をしておけば，対応づけだけでどのシステムにもその考え方が適用できる。
| 機械系（直線運動） | 機械系（回転運動） | 電気系 | 熱系 |
|---|---|---|---|
| 力 $f$ [N] | トルク $\tau$ [N·] | 電圧 $v$ [V] | 温度 $\theta$ [K] |
| 位置 $x$ [m] | 回転角 $\theta$ [rad] | 電荷 $q$ [C] | 熱量 $Q$ [J] |
| 速度 $v$ [m/s] | 回転角速度 $\omega$ [rad/s] | 電流 $i$ [A] | 熱流量 $q$ [J/s] |
| 質量 $M$ [kg] | 慣性モーメント $J$ [kg·m2] | インダクタンス $L$ [H] | - |
| 粘性減衰係数 $D$ [N·s/m] | 粘性摩擦係数 $B$ [N·m·s/rad] | 抵抗 $R$ [Ω] | 熱抵抗 $R$ [K·s/J] |
| ばね定数 $K$ [N/m] | ばね定数 $K$ [N·m/rad] | 静電容量 $C$ [F] | 熱容量 $C$ [J/K] |
なお，システムのモデル化の流れは次の通り。
- 入出力をともなう物理システム（機械系，電気系など）
- 注目する変数の変化の様子について，微分方程式で記述
- 微分方程式をラプラス変換し，伝達関数でシステムの特性を記述
- システム同士の結合をブロック線図をもとに行う
- 複雑なシステムの入出力関係，特性が明らかになる
電気系
オームの法則がラプラス変換によって保存されることは，線形則より明らかであるが，容量素子および誘導素子にかかわる方程式もラプラス変換によって電圧 $V(s) = \mathcal{L}[v(t)]$ と電流 $I(s) = \mathcal{L}[i(t)]$ の間の線形な関係式に帰着させることができる。
容量素子
静電容量 $C$ を持つ容量素子の特性は，電荷 $q(t)$ を介して
\[ i(t)=\frac{\text{d}q(t)}{\text{d}t}=C\frac{\text{d}v(t)}{\text{d}t} \]と表される。この両辺をラプラス変換し，$t$ 関数の微分の公式を適用すれば
\[ I(s)=sCV(s)-Cv(0) \]となる。ここで，初期電荷 $q(0) = Cv(0) = 0$ とすれば，次式が成り立つ。
\[ \frac{V(s)}{I(s)}=\frac{1}{sC} \]容量素子はインピーダンス $\displaystyle Z(s)= \frac{1}{sC}$（アドミタンス $Y(s) = sC$）を持つ素子と解釈できる。
誘導素子
インダクタンス $L$ を持つ誘導素子の特性は，磁束 $\phi(t)$ を介して
\[ v(t)=\frac{\text{d}\phi(t)}{\text{d}t}=L\frac{\text{d}i(t)}{\text{d}t} \]と表されるので，ラプラス変換によって $s$ 関数で表せば
\[ V(s)=sLI(s)-Li(0) \]となる。ここで，初期磁束 $\phi(0) = Li(0)$ とすれば，次式が成り立つ。
\[ \frac{V(s)}{I(s)}=sL \]誘導素子はインピーダンス $Z(s)=sL$ を持つ素子と解釈できる。
参考文献
- 北川 能，掘込 泰雄，小川 侑一 共著，「自動制御工学」，森北出版，2004年3月15日 第 1 版第 3 刷
- 佐藤 和也，平元 和彦，平田 研二 著，「はじめての制御工学」，講談社，2010年10月20日 第 1 刷発行，2012年6月10日 第 4 刷発行
- 佐々木 清吾 著，「電気電子システムのための制御工学」，電気学会
- JIS Z 8116 : 1994「自動制御用語 - 一般」
- 平山 博，大附 辰夫 著，「電気学会大学講座 電気回路論 ［２版改訂］」，電気学会，2002年12月25日 2 版改訂 1 刷発行
- 山崎 亨 著，「情報工学のための電子回路」，森北出版，2015年3月5日 第 1 版第 3 刷
- 水本 哲弥 著，「フーリエ級数・変換／ラプラス変換」，オーム社，2010年5月10日 第 1 版第 1 刷
- 「電気学会大学講座 電気・電子基礎数学 − 電磁気，回路のための −」，社団法人 電気学会，1980年9月12日 初版1刷発行，2004年2月20日 21刷発行
- 機械工学辞典 Mechanical Engineering Dictionary
はじめての制御工学
制御工学，よりわけ古典制御の内容について，初学者が理解しやすくなるように心がけて執筆されている。特に，制御工学を理解するための数式の読みとり方，意味などの説明に重点が置かれている。（336ページ，講談社，2018年11月19日発売）
- 講義01 制御とは～微分方程式とのつながり～
- 講義02 システムの数学モデル
- 講義03 伝達関数の役割
- 講義04 動的システムの応答
- 講義05 システムの応答特性
- 講義06 2 次遅れ系の応答
- 講義07 極と安定性
- 講義08 制御系の構成とその安定性
- 講義09 PID 制御
- 講義10 フィードバック制御系の定常特性
- 講義11 周波数応答の解析
- 講義12 ボード線図の特性と周波数伝達関数
- 講義13 ナイキストの安定性判別法
- 講義14 ループ整形法によるフィードバック制御系の設計
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1ee2a380.5327b49b.1ee2a381.6d6071b3/?me_id=1213310&item_id=19319273&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F7475%2F9784065137475.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
電気電子システムのための制御工学
大学の学部で習う基礎的な内容が詰まっている $RLC$ 直列回路を通じて制御工学を学ぶ，新しい視点に立った教科書である。$RLC$ 直列回路の基礎をもとに現代制御を主に，古典制御を従にして制御工学が理解できるようになっている。後半では，電気電子システムの解析・設計を通じて，制御工学の理解を深められるようになっている。（208ページ，電気学会，2017年12月16日発売）
- 第1章 解析・設計手法に応じたシステムのモデル化
- 第2章 時間領域でのシステム解析
- 第3章 周波数領域でのシステム解析
- 第4章 時間領域での制御系設計
- 第5章 周波数領域での制御系設計
- 第6章 電気電子システムへの制御工学的接近
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1ee2a380.5327b49b.1ee2a381.6d6071b3/?me_id=1213310&item_id=18900729&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3096%2F9784886863096.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
PID 制御 現代制御論の観点から
フィードバック制御の定番である PID 制御を，伝達関数で表現する古典制御ではなく，状態方程式に基づく現代制御の観点から解説したものである。今も広く用いられている PID 制御を現代制御の視点から解説することで，より詳細かつ複雑な解析を行うための知識を提供する。高度かつ理論的に，具体的な制御器に落とし込むことができ，実際に応用可能な制御理論を紹介する。（312ページ，オーム社，2020年11月6日発売）
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1ee2a380.5327b49b.1ee2a381.6d6071b3/?me_id=1213310&item_id=20151175&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6304%2F9784274226304.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")