電気通信システム対策ノート「電子回路・ディジタル回路」

2019年5月18日作成，2021年9月1日更新

電子回路・ディジタル回路

ダイオードとトランジスタ

ダイオード

pn 接合形ダイオードは増幅機能をもたない非線形回路素子であり，pn 接合では電流を一方向にしか流さない。これを整流作用といい，整流作用を示す回路素子をダイオード（diode）または整流器と呼ぶ。

ダイオードは理想的には順方向抵抗が 0，逆方向抵抗が無限大の非線形素子とみなされ，下図の記号で表される。

バラクタダイオード（日本ではバリキャップと呼ぶことが多い）は，可変容量ダイオードのことである。pn 接合部に逆バイアスをかけて静電容量をバイアス電圧により抑制する。バイアス電圧が低いと空乏層が狭まり，容量が増加する。バイアス電圧を下げると上げると空乏層が広がり，容量が低下する。通常，空乏層の幅は印加電圧の平方根に比例し，静電容量は空乏層の幅に反比例する。このため，静電容量は印加電圧の平方根に反比例する。

静電容量がバイアス電圧により大きく変化することを利用して，VCO（電圧制御発振器），電子同調，周波数逓倍などに用いられる。

トランジスタ

p 形半導体と n 形半導体をサンドイッチ状に重ね，二つの pn 接合を形成したトランジスタを接合型トランジスタ（junction transistor）またはバイポーラトランジスタという。この形式のトランジスタには p 形と n 形の配置によって pnp 形と npn 形がある。

npn 形トランジスタは p 形半導体を n 形半導体ではさみこむように作られ，それぞれに電極がつけられている。これらの三つの領域は左から順にキャリアを発生させる意味でエミッタ（emitter），電位の基準の意味でベース（base），キャリアを集める意味でコレクタ（collector）と呼ばれ，それぞれ記号 E，B，C で表される。なお，図中の右側はトランジスタを表す記号であるが，円形の囲いを省略して使われることもある。また，矢印の向きは，エミッタ電流の向きを表す。

増幅回路

アナログ電子回路にはさまざまな機能をもつものがあるが，これらのうちもっとも重要なのは信号を増幅する機能をもつ増幅器（amplifier）である。増幅器には，かつては真空管が使われていたが，今日ではほとんどの場合にトランジスタが使われている。

増幅器はいろいろな観点から分類されるが，それらのうちでもっとも重要なのは扱われる信号の交・直流の違いであり，交流増幅器（ac amplifier）と直流増幅器（dc amplifier）に分類される。

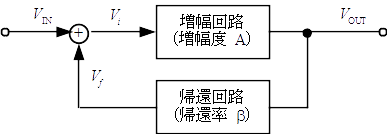
帰還増幅回路

帰還増幅回路には，正帰還回路と負帰還回路がある。負帰還（negative feedback）は出力信号の一部を，極性を反転して入力側に戻す回路であり，特徴として，増幅器の増幅度は小さくなるが，周波数特性を改善することができる。

一方，出力信号の一部を同一極性で入力回路に戻すことを正帰還（positive feedback）といい，増幅器の出力を増大することができるが，周波数帯域は狭くなり，帰還量を一定以上増やす（ループゲインが 1 以上になる）と発振状態になる。

発振回路

帰還増幅器では $1 - \beta A = 0$ のときには回路が発振する。この現象は通常の電子回路では不都合なことが多いが，うまく利用すると外部から信号を加えなくても希望する信号を発生させ，取り出すことができる。この回路を発振器（oscillator）という。

変復調回路

音声信号などの低周波電圧信号はそのままでは空間を遠方まで伝搬させるには適さない。このため，高周波電圧の振幅，周波数あるいは位相を低周波信号の特徴によって変化させ，この高周波電圧を伝搬させる。これを変調（modulation）といい，低周波電圧信号を変調信号（modulation signal），高周波信号を搬送波（carrier），変調された信号を変調波（modulated wave）という。

変調によって得られた信号，すなわち変調波は伝搬されたのち，変調信号となった低周波信号を再現する信号が抽出される。これを復調（demodultation）という。

変調速度

変調過程において 1 秒間に状態が変化した回数を表すもので，単位は [ボー] である。

変調器

搬送波が変調信号のどのような特徴によって変調されるかによって，変調器には主として以下の 3 方式がある。

振幅変調（amplitude modulation : AM）
周波数変調（frequency modulation : FM）
位相変調（phase modulation : PM）

このうち，周波数と位相角を変化させる方式は，総称して角度変調という。

復調器

変調波からもとの変調信号を取り出す操作を復調，または検波という。

この回路は PLL（Phase Locked Loop : 位相同期回路）といわれる。入力される周期的な信号を元にフィードバック制御を加え，位相同期した信号を出力する回路である。フィードバックに加える信号を制御して，色々な信号を安定して作り出すことができる。

A/D・D/A 変換回路

われわれが物理現象から得るデータのほとんどはアナログ量（analog quantity）である。しかし，これを処理して，種々の有益な情報を得るにはアナログの手法よりディジタルの手法が適する場合が多い。ディジタルデータ処理のためには，まず対象となるアナログ量から標本を抽出し，それをディジタル信号（digital signal）に変換する。そして，ディジタル装置によって処理されたデータは最終的にはそのまま表示，記録されたり，制御に使われることも多いが，アナログ量に変換してから表示されたり，制御に使われる場合がある。

A/D 変換（analog - to - digital conversion）

アナログ量のディジタル量への変換器（converter）によって行われる。

PAM（Pulse Amplitude Modulation）：パルス振幅変調方式
PWM（Pulse Width Modulation）：パルス幅変調方式
PPM（Pulse Position Modulation）：パルス位置変調方式
PFM（Pulse Frequency Modulation）：パルス周波数変調方式
PCM（Pulse Code Modulation）：パルス符号変調方式

量子化雑音を小さくする方法として非直線量子化がある。非直線量子化は信号レベルが小さいときは量子化ステップを小さく，信号レベルが大きいときは量子化ステップの幅を大きくする方法である。具体的には，入力信号を圧縮した後で，均一量子化を行う。受信側では直線量子化の復号器の後で伸張器を通すことにより，圧縮された信号を引き伸ばし，元の量子化信号を得ることができる。

非直線量子化

PCM（Pulse Code Modulation）方式で音声信号を伝送する場合，125 μs 単位に標本化して PAM（Pulse-Amplitude Modulation）パルスを得る。次段階で PAM パルスを量子化するが，この際，量子化雑音（まるめ誤差）が生じる。この雑音を抑えるため，一般に信号振幅が小さいときは量子化ステップを小さく，信号振幅が大きいときは量子化ステップを大きくとり，小振幅域と大振幅域での SN 比を近づけるような非直線量子化が用いられている。

予測符号化

予測符号化とは，着目している音声や画素などと空間的・時間的に近い位置にある音声信号，画素の値から，予測関数に従って対象信号値を予測し，このときの予測値と実際の値との差異（予測誤差）を符号化する手法の総称である。予測関数が十分に正確であれば，予測誤差は 0 に近い値をとる可能性が高く，この誤差に対して変換，量子化及びエントロピー符号を適用することで大幅な圧縮効率の向上が期待できる。

D/A 変換（digital - to - analog conversion）

ディジタル量からアナログ量への変換器によって行われる。

基本論理演算

論理代数の定義

$x$ が論理値（switching value）をもつとは，$x$ が 0，1 のどちらかの値を取ること，すなわち，次式が成り立つ。

$x \neq 0$ ならば $x = 1$

$x \neq 1$ ならば $x = 0$

このような 2 値の論理値を，真理値（truth value）あるいはブール値（Boolcan value）と呼ぶこともある。

論理代数（switching algebra）は，論理値 (0,1) に関する，論理積（AND），論理和（OR），否定（NOT）の三つの演算からなる代数系として定義される。ここで，論理積，論理和，否定は以下のように定義される二項演算及び単項演算である。

表論理積，論理和，否定
$x$	$y$	$x \cdot y$	$x + y$	$\overline{x}$
0	0	0	0	1
0	1	0	1	1
1	0	0	1	0
1	1	1	1	0

論理代数の性質

論理代数は，以下に示す法則を満たす。

べき等則（idempotency）
$ x \cdot x = x$ ，$ x + x = x$
零元（zero element）
$x \cdot 0 = 0$ ，$x + 1 = 1$
単位元（identity element）
$x \cdot 1 = x$ ，$x + 0 = x$
交換則（comutativity）
$x \cdot y = y \cdot x$ ，$x + y = y + x$
結合則（associativity）
$(x \cdot y) \cdot z = x \cdot (y \cdot z)$ ，$(x + y ) + z = x + (y + z)$
相補則（complementation）
$x \cdot \overline{x} = 0$ ，$x + \overline{x} = 1$
分配則（distributivity）
$x \cdot (y + z) = (x \cdot y) + (x \cdot z)$ ，$x + (y \cdot z) = (x + y)\cdot(x + z)$
吸収則（absorption）
$x + (x \cdot y) = x$ ，$x \cdot (x + y) = x$
二重否定則（involution）
$\overline{\overline{x}} = x$
ド・モルガンの法則（De Morgan's laws）
$\overline{x + y} = \overline{x}\cdot\overline{y}$ ，$\overline{x \cdot y} = \overline{x} + \overline{y}$

組合せ回路

組合せ回路は，NOT，AND，OR などの基本的な論理関数を計算する論理ゲートと，それらを接続する配線からなる，フィードバックループをもたない回路である。いくつかの入力と出力をもち，各入出力は 0 または 1 の値を取る。各出力の値は，入力の値の組合せのみにより一意に定まる。すなわち，組合せ回路は論理関数を計算している。組合せ回路がある論理関数を計算しているとき，その論理関数を実現しているという。

NAND 回路

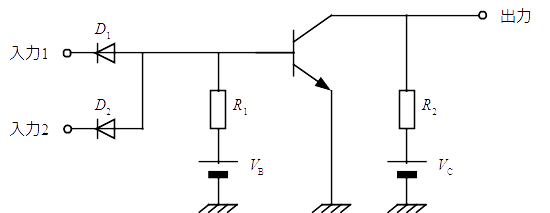
真理値表は以下の通りとなり，NAND 回路を示している。

表真理値表
入力 1	入力 2	$D_1$，$D_2$ とトランジスタのベース電圧	トランジスタの状態	出力
0	0	$D_1$，$D_2$ ともオンのため，ベース電圧は 0 [V]	オフ	1
0	1	$D_1$ がオンのため，ベース電圧は 0 [V]	オフ	1
1	0	$D_2$ がオンのため，ベース電圧は 0 [V]	オフ	1
1	1	$D_1$，$D_2$ ともオフのため，ベース電圧は $V_B$ [V]	オン	0

フリップフロップ

フリップフロップ（flip - flop）は，二進法の基本である 1 ビットの情報を一時的に 0 または 1 の状態として保持する（記憶する）ことができる論理回路で，順序回路の基本要素である。

順序回路

順序回路は過去の内部状態と取得時の入力信号とで出力が決まる回路である。組み合わせ回路は，伝搬遅延によって信号が遅れることを除けば，入力の組み合わせだけで出力が一意に決まるが，順序回路はループにより内部に状態を保持しており，過去の入力に影響されるその状態も，出力の決定に関わる。

記憶回路

半導体メモリには，読み出しと書き込みが可能な RAM（Random Access Memory）と，読み出しのみ可能な ROM（Read Only Memory）がある。またデータの記憶に電源を必要とする揮発メモリと電源を必要としない不揮発メモリがある。

揮発メモリである RAM には DRAM（Dynamic RAM）と SRAM（Static RAM）がある。DRAM はトランジスタ 1 個とコンデンサ 1 個で 1 ビットのメモリが構成されるが，コンデンサは時間とともに自然放電するので，再書き込みが必要になる。一方，SRAM は 4 ～ 6 個のトランジスタからなるフリップフロップ回路によって構成され，電源の供給を続ければ再書き込みは不要である。

電気通信システム 対策ノート「電子回路・ディジタル回路」